

���� ��1�����A��B��ĺ����꣬����S��OAB=S��AOC-S��BOC���㼴�ɣ�
��2�����÷������Լ�����ϵ���Ĺ�ϵ�����AB������AB=$\frac{5}{2}$$\sqrt{2}$���г����̼��ɽ�����⣮
��3������֤��PM=PF���Ƴ�PM+PN=PF+PN��NF=2�Ƴ�����P��NF��ʱ�Ⱥų�������ʱNF�ķ���Ϊy=-x+2$\sqrt{2}$���ɣ�1��֪P��$\sqrt{2}$-1��$\sqrt{2}$+1�����ɴ˼��ɽ�����⣮
��� ��𣺽⣺��1����k=-1ʱ��l1��y=-x+2$\sqrt{2}$��
�����ã�$\left\{\begin{array}{l}{y=-x+2\sqrt{2}}\\{y=\frac{1}{x}}\end{array}\right.$�������x2-2$\sqrt{2}$x+1=0��
��ã�x1=$\sqrt{2}$-1��x2=$\sqrt{2}$+1��
��ֱ��l1��y�ύ�ڵ�C����C��0��2$\sqrt{2}$����
S��OAB=S��AOC-S��BOC=$\frac{1}{2}$•2$\sqrt{2}$•��x2-x1��=2$\sqrt{2}$��
��2����������ã�$\left\{\begin{array}{l}{y-\sqrt{2}=k��x-\sqrt{2}��}\\{y=\frac{1}{x}}\end{array}\right.$ �����ã�kx2+$\sqrt{2}$��1-k��x-1=0��k��0����
�ߡ�=[$\sqrt{2}$��1-k��]2-4��k����-1��=2��1+k2����0��
��x1��x2 �Ƿ��̵�������
��$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{\sqrt{2}��k-1��}{k}}\\{{x}_{1}•{x}_{2}=-\frac{1}{k}}\end{array}\right.$ �٣�
��AB=$\sqrt{��{x}_{1}-{x}_{2}��^{2}+��{y}_{1}-{y}_{2}��^{2}}$=$\sqrt{��{x}_{1}-{x}_{2}��^{2}+��\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}��^{2}}$��
=$\sqrt{��{x}_{1}-{x}_{2}��^{2}[1+��\frac{1}{{x}_{1}{x}_{2}}��^{2}]}$��
=$\sqrt{[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}][1+��\frac{1}{{x}_{1}{x}_{2}}��^{2}]}$��
���ٴ���ã�AB=$\sqrt{\frac{2��{k}^{2}+1��^{2}}{{k}^{2}}}$=$\frac{\sqrt{2}��{k}^{2}+1��}{-k}$��k��0����
��$\frac{\sqrt{2}��{k}^{2}+1��}{-k}$=$\frac{5\sqrt{2}}{2}$��
�����ã�2k2+5k+2=0��
��ã�k=-2���� k=-$\frac{1}{2}$��
��3����y-$\sqrt{2}$=k��x-$\sqrt{2}$����k��0��������F��
��x=$\sqrt{2}$��y=$\sqrt{2}$��
��F��$\sqrt{2}$��$\sqrt{2}$����
��P��x��$\frac{1}{x}$������M��-$\frac{1}{x}$+$\sqrt{2}$��$\frac{1}{x}$����
��PM=x+$\frac{1}{x}$-$\sqrt{2}$=$\sqrt{��x+\frac{1}{x}-\sqrt{2}��^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}��x+\frac{1}{x}��+4}$��
��PF=$\sqrt{��x-\sqrt{2}��^{2}+��\frac{1}{x}-\sqrt{2}��^{2}}$=$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2\sqrt{2}��x+\frac{1}{x}��+4}$��
��PM=PF��
��PM+PN=PF+PN��NF=2��
����P��NF��ʱ�Ⱥų�������ʱNF�ķ���Ϊy=-x+2$\sqrt{2}$��
�ɣ�1��֪P��$\sqrt{2}$-1��$\sqrt{2}$+1����
�൱P��$\sqrt{2}$-1��$\sqrt{2}$+1��ʱ��PM+PN��С����ʱ�ı���QMPN���ܳ���С��ƽ���ı��Σ�
��Q��-$\sqrt{2}$��2 $\sqrt{2}$����
���� ���⿼�鷴���������ۺ��⡢һ�κ��������ʡ�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ���������빫ʽ��ƽ���ı��ε����ʵ�֪ʶ������Ĺؼ���ѧ�����÷����������������Ľ������ꡢѧ�����ò������������̽�����⣬ѧ����������֮���߶���̽��������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9800��ѧ�������� | |
| B�� | ÿ��ѧ���Ǹ��� | |
| C�� | 100��ѧ��������ȡ��һ������ | |
| D�� | 100��ѧ�����������������ȡ��һ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����C�ǰ�ԲO�ϵ�һ�㣬ACƽ�֡�DAB��AD��CD������ΪD��AD����O�ڵ�E������CE��
��ͼ��AB�ǡ�O��ֱ����C�ǰ�ԲO�ϵ�һ�㣬ACƽ�֡�DAB��AD��CD������ΪD��AD����O�ڵ�E������CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
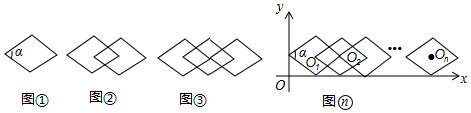
| ͼ������ | ����ͼ�εĸ��� | ���εĸ��� |
| ͼ�� | 1 | 1 |
| ͼ�� | 2 | 3 |
| ͼ�� | 3 | 7 |
| ͼ�� | 4 | 11 |
| �� | �� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
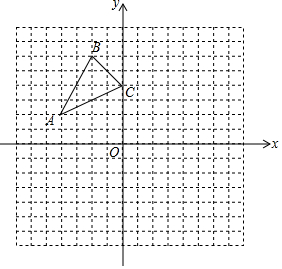 ��ͼ����֪A ��-4��2����B ��-2��6����C ��0��4����ֱ������ϵƽ�������㣮
��ͼ����֪A ��-4��2����B ��-2��6����C ��0��4����ֱ������ϵƽ�������㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com