
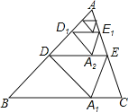
����Ŀ����ͼ������ABC���Ź�AB�е�D��ֱ���۵���ʹ��A����BC���ϵ�A1����Ϊ��1�β������ۺ�DE��BC�ľ����Ϊh1����ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2������Ϊ��2�β������ۺ�D1E1��BC�ľ����Ϊh2���������������ϲ�����ȥ����������2019�β�����õ����ۺ�D2018E2018����BC�ľ����Ϊh2019����h1��1����h2019��ֵΪ��____��
���𰸡�2��![]()
��������
�����е�����ʼ��۵������ʿɵ�DA��DA'��DB���Ӷ��ɵá�ADA'��2��B������۵������ʿɵá�ADA'��2��ADE���ɵá�ADE����B���̶��ж�DE��BC���ó�DE����ABC����λ�ߣ�֤��AA1��BC���õ�AA1��2�����h1��21��1��ͬ����h2��2![]() ��h3��2
��h3��2![]() ��
��![]() ��2
��2![]() ��������n�β�����õ����ۺ�Dn1En1��BC�ľ���hn��2
��������n�β�����õ����ۺ�Dn1En1��BC�ľ���hn��2![]() ��
��
�⣺���۵������ʿɵã�AA1��DE��DA��DA1��
�֡�D��AB�е㣬
��DA��DB��
��DB��DA1��
���BA1D����B��
���ADA1��2��B��
�֡ߡ�ADA1��2��ADE��
���ADE����B��
��DE��BC��
��AA1��BC��
��AA1��2h1��2��
��h1��21��1��
ͬ����h2��2![]() ��h3��2
��h3��2![]() ��
��![]() ��2
��2![]() ��
��
�ྭ����n�β�����õ����ۺ�Dn1En1��BC�ľ���hn��2![]() ��
��
��h2019��2![]() ��
��
�ʴ�Ϊ��2![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
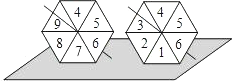
����Ŀ����ͼ��ʾ��С����С����ת������Ϸ������ͬʱ�ֱ�ת��һ�����ݣ����������ݶ�ͣ����ʱ����������Ӵ��ı��ϵ����ֶ��������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
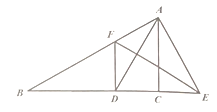
����Ŀ����ͼ��һ���������˶������ָ���A��B��A��B��C��5������A���DZ߳�Ϊa m�������Σ�C���DZ߳�Ϊc m�������Σ�
(1)��ʽ��ʾÿ��B�������γ��ص��ܳ�������ʽ�ӻ���
(2)��ʽ��ʾ�����������˶������ܳ�������ʽ�ӻ���
(3)���a��40��c��10���������������˶����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ��ABC�У�AB=AC����A=36�㣬AC�Ĵ�ֱƽ���߽�AB��E��DΪ���㣬����EC
�����ECD�Ķ�����
����CE=5����CB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨѶ�г����������漤�ң�Ϊ��ռ���г�����˾�Ƴ����Żݴ�ʩ�ǣ�ÿ���ӽ���![]() Ԫ�����µ�
Ԫ�����µ�![]() ���ҹ�˾�Ƴ����Żݴ�ʩ�ǣ�ÿ�����µ�
���ҹ�˾�Ƴ����Żݴ�ʩ�ǣ�ÿ�����µ�![]() ���ٽ���
���ٽ���![]() Ԫ.��֪�ס�������˾ԭ��ÿ�����շѱ���ͬ������
Ԫ.��֪�ס�������˾ԭ��ÿ�����շѱ���ͬ������![]() Ԫ.
Ԫ.
��1���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ�ס�������˾�Ƴ��Żݴ�ʩ��ÿ���ӵ��շѱ���
��ʽ�ӱ�ʾ�ס�������˾�Ƴ��Żݴ�ʩ��ÿ���ӵ��շѱ���
��2���Ƴ��Żݴ�ʩ���ļҹ�˾���շѱ��ˣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��ʾ���߶�![]() ����
����![]() ���߶�
���߶�![]() ��һ�㣬
��һ�㣬![]() �ֱ����߶�
�ֱ����߶�![]() ���е㣬С���ݴ˺����ɵ����
���е㣬С���ݴ˺����ɵ����![]() ����֪��С�������������������д�������̣�
����֪��С�������������������д�������̣�
![]()
��2��С����˼������ͻ�����룺����![]() ��
��![]() ���ӳ�����ʱ��ԭ�еĽ��ۡ�
���ӳ�����ʱ��ԭ�еĽ��ۡ�![]() ���Ƿ���Ȼ���������С������ͼ�β�˵�����ɣ�
���Ƿ���Ȼ���������С������ͼ�β�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�
��![]() ��
��![]() ƽ���ߣ�
ƽ���ߣ�![]() �Ĵ�ֱƽ���߷ֱ�
�Ĵ�ֱƽ���߷ֱ�![]() �ӳ����ڵ�
�ӳ����ڵ�![]() .��֤��
.��֤��![]() .
.
֤������![]() ƽ��
ƽ��![]()
��![]()
![]() (��ƽ���ߵĶ���)
(��ƽ���ߵĶ���)
��![]() ��ֱƽ��
��ֱƽ��![]()
�� ![]() ���߶δ�ֱƽ�����ϵĵ㵽�߶������˵������ȣ�
���߶δ�ֱƽ�����ϵĵ㵽�߶������˵������ȣ�
��![]() �� ��
�� ��
��![]() ������������
������������
��![]() �� ��
�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�鳤5��4�ĵ�̺��Ϊ��������������ᡢ���ݵ���ɫ���ƣ�ͼ����Ӱ���֣�����֪��ɫ���ƵĿ�����ͬ����ռ�����������̺�����![]() ��
��
��1������ɫ���ƵĿ��ȣ�
��2�������̺��ɫ���Ʋ���ÿƽ�������200Ԫ�����ಿ��ÿƽ�������100Ԫ�����̺������ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB��AC��10cm��BC��8cm����DΪAB���е㣮�����P���߶�BC����3cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�CA���ɵ�C��A���˶���
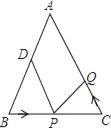
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com