
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=24 cm,BC=26 cm.点P从A出发,以1 cm/s的速度向点D运动,点Q从点C同时出发,以3 cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD需要__________秒
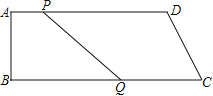
【答案】6或7
【解析】当PD=CQ时可知四边形PQCD为平行四边形或四边形PQCD为等腰梯形,根据它们的性质可建立关于t的方程,解出即可.
(1)当PD=CQ时,四边形PQCD是平行四边形;
设运动时间为t秒,
∴24-t=3t
解得t=6s,
(2)当四边形PQCD是等腰梯形时,PQ=CD.
设运动时间为t秒,则有AP=tcm,CQ=3tcm,
∴BQ=26-3t,
作PM⊥BC于M,DN⊥BC于N,则有NC=BC-AD=26-24=2.
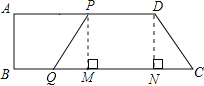
∵梯形PQCD为等腰梯形,
∴NC=QM=2,
∴BM=(26-3t)+2=28-3t,
∴当AP=BM,即t=28-3t,解得t=7,
∴t=7时,四边形PQCD为等腰梯形.
综上所述t=6s或7s时,PQ=CD.
故答案为6s或7s.


科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:

(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图1,已知点A是BC外一点,连接AB,AC,求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程
解:过点A作ED∥BC
∴∠B=∠ ,∠C=∠ .
又∵∠EAB+∠BAC+∠DAC=180°(平角定义)
∴∠B+∠BAC+∠C=180°
从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
小明受到启发,过点C作CF∥AB如图所示,请你帮助小明完成解答:
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°.BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间.
①如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 °.
②如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 °(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线![]() (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
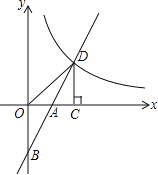
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
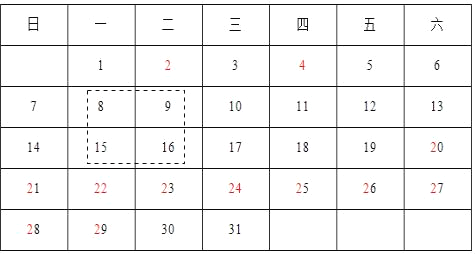
【题目】如图所示为2013年7月份的日历示意图.
(1)请你计算虚线方框圈出的2×2个数(2行2列的4个数)的和;
(2)若方框圈出的2×2个数从左下角到右上角的2个数之和为46,则这4个数的最后一天是7月 日.(直接填空)
(3)若方框圈出的2×2个数的和最大,请你用方框将这4个数圈出来,并计算这4个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c(a≠0)与x轴、y轴分别交于点A(3,0)、B(0,3)两点.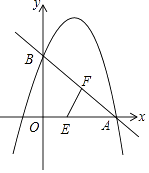
(1)试求抛物线的解析式和直线AB的解析式;
(2)动点E从O点沿OA方向以1个单位/秒的速度向终点A匀速运动,同时动点F沿AB方向以 ![]() 个单位/秒的速度向终点B匀速运动,E、F任意一点到达终点时另一个点停止运动,连接EF,设运动时间为t,当t为何值时△AEF为直角三角形?
个单位/秒的速度向终点B匀速运动,E、F任意一点到达终点时另一个点停止运动,连接EF,设运动时间为t,当t为何值时△AEF为直角三角形?
(3)抛物线位于第一象限的图象上是否存在一点P,使△PAB面积最大?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2 ![]() ,sin∠AOC=
,sin∠AOC= ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点C以及边AB的中点D.
的图象经过点C以及边AB的中点D. 
(1)求这个反比例函数的解析式;
(2)四边形OABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com