
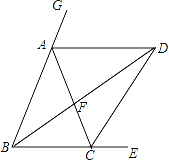
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.
(1)求证:∠BDC=![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
【答案】(1)证明详见解析;(2)△ABD为等腰三角形,理由详见解析;(3)72°.
【解析】
试题分析:(1)根据角平分线的定义得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ACE,∠BAC+∠ABC=∠ACE,于是得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠BAC+
∠BAC+![]() ∠ABC,等量代换即可得到结论;
∠ABC,等量代换即可得到结论;
(2)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H,根据角平分线的性质得到DM=DH,DN=DH,等量代换得到DM=DN,根据三角形的内角和得到∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,推出∠GAD+∠CAD=∠ABC+∠ACB,由等腰三角形的性质得到∠ABC=∠ACB,等量代换得到∠GAD=∠ABC,推出AD∥BC,由平行线的性质得到∠ADB=∠DBC,证得∠ABD=∠ADB,即可得到结论;
(3)根据等腰三角形的性质得到∠BAF=∠ABF=![]() ∠ABC,根据三角形的内角和即可得到结论.
∠ABC,根据三角形的内角和即可得到结论.
试题解析:(1)∵BD、CD分别平分∠EBA、∠ECA,BD交AC于F,
∴∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ACE,∠BAC+∠ABC=∠ACE,
∠ACE,∠BAC+∠ABC=∠ACE,
∴∠BDC+![]() ∠ABC=
∠ABC=![]() ∠BAC+
∠BAC+![]() ∠ABC,
∠ABC,
∴∠BDC=![]() ∠BAC;
∠BAC;
(2)△ABD为等腰三角形,证明如下:
作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H
∵BD、CD分别平分∠EBA、∠ECA,
∴DM=DH,DN=DH,
∴DM=DN,
∴AD平分∠CAG,即∠GAD=∠CAD,
∵∠GAD+∠CAD+∠BAC=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠GAD+∠CAD=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC,
∴∠ADB=∠DBC,
又∵∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴△ABD为等腰三角形;
(3)∵AF=BF,
∴∠BAF=∠ABF=![]() ∠ABC,
∠ABC,
∵∠BAF+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°.



科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. ﹣2的相反数是2 B. 3﹢(﹣3)﹦0
C. (﹣3)﹣(﹣5)=2 D. ﹣11,0,4这三个数中最小的数是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是
A. 等腰三角形一腰的长至少要大于底边长的一半
B. 三角形按边的关系分为不等边三角形、等边三角形
C. 长度为5、6、10的三条线段不能组成三角形
D. 等腰三角形的两边长是1和2,则其周长为4或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在黑板上写有若干个有理数.若他第一次擦去m个,从第二次起,每次都比前一次多擦去2个,则5次刚好擦完;若他每次都擦去m个,则10次刚好擦完.则小明在黑板上共写了________个有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、以两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com