
 一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°.若AB=4,则S△BCD=$\frac{3\sqrt{3}-3}{2}$(结果保留根号)
一副三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°.若AB=4,则S△BCD=$\frac{3\sqrt{3}-3}{2}$(结果保留根号) 分析 作BH⊥CF于H,根据直角三角形的性质、勾股定理分别求出AC、BC、BH、DC,根据三角形的面积公式计算即可.
解答 解: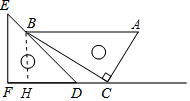 作BH⊥CF于H,
作BH⊥CF于H,
∵∠ACB=90°,∠A=60°,
∴∠ABC=30°,
∴AC=$\frac{1}{2}$AB=2,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∵AB∥CF,
∴∠BCH=∠ABC=30°,
∴BH=$\frac{1}{2}$BC=$\sqrt{3}$,
∴HC=$\sqrt{B{C}^{2}-B{H}^{2}}$=3,
∵∠E=45°,
∴HD=BH=$\sqrt{3}$,
∴DC=3-$\sqrt{3}$,
∴S△BCD=$\frac{1}{2}$×(3-$\sqrt{3}$)×$\sqrt{3}$=$\frac{3\sqrt{3}-3}{2}$.
故答案为:$\frac{3\sqrt{3}-3}{2}$.
点评 本题考查的是勾股定理的应用,掌握如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,BC=20cm,D是AB上一点,且CD=16cm,BD=12cm.
如图,在△ABC中,AB=AC,BC=20cm,D是AB上一点,且CD=16cm,BD=12cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
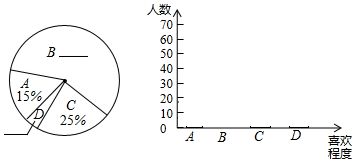 某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表. | 喜欢程度 | 频数 |
| A | 18 |
| B | 66 |
| C | 30 |
| D | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
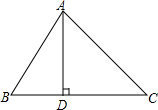 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
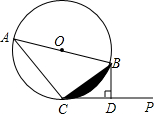 已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com