
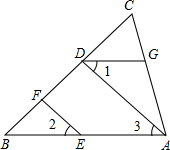
 如图,已知EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.
如图,已知EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°. 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
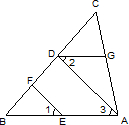 19、如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.
19、如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省建德市李家镇初级中学七年级3月月考数学试卷(带解析) 题型:解答题
如图,已知EF∥AD,∠1=∠2,∠BAC=65º.请将求∠AGD的过程填写完整.
解:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源:2015届浙江省建德市七年级3月月考数学试卷(解析版) 题型:解答题
如图,已知EF∥AD,∠1=∠2,∠BAC=65º.请将求∠AGD的过程填写完整.
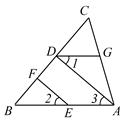
解:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江临安於潜第一初级中学八年级10月数学试卷(解析版) 题型:解答题
如图,已知EF∥AD,∠1 =∠2,∠BAC=65º.请将求∠AGD的过程填写完整.
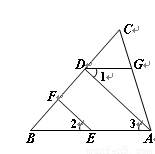
解:∵EF∥AD( )
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com