Question

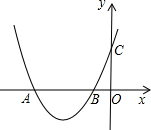
12．已知：如图，抛物线y=ax²+4ax+c，与x轴负半轴交于A、B，与y轴正半轴交于C，OC=3，AB=2，
（1）求抛物线的解析式；
（2）点P为第二象限对称轴左侧抛物线上一点，过P作x轴的垂线垂足为G，连接AC，E为线段AC上一点，连接EG，将EG绕着E点顺时针旋转90°，得到EN，连接NA，求证：PG∥NA；
（3）在（2）的条件下，延长NE到F，使EN=EF，过F点作y轴的垂线FM，连接PE、PC，若直线FM经过抛物线的顶点D，连接BC，∠EPC+90°=∠ABC，求E点的坐标．

Answer 1

分析 （1）求出抛物线的对称轴x=-1，根据条件可知A（-3，0），B（-1，0），再利用待定系数法即可解决问题．
（2）如图1中，过E作EM⊥AB于M，作NK⊥EM于K．先证明△ENK≌△GEM，得NK=EM，推出四边形ANKM是矩形，由此即可解决问题．
（3）如图2中，连接GN、GF，作EK⊥PC于K，FH⊥x轴于H，由△AGN≌△FHG，推出AG=FH，推出P（-4，3），推出四边形PGOC是矩形，由tan∠EPC=tan∠BCO=$\frac{BO}{CO}$=$\frac{1}{3}$=$\frac{KE}{PK}$，推出PK=3EK，由∠KCE=∠ECO=45°，推出KE=KC，推出PK=3KC，推出KC=1，由此即可解决问题．

解答 解：（1）对于抛物线y=ax²+4ax+c，
∵对称轴x=-2，AB=2，OC=3，
∴c=3，A（-3，0），B（-1，0），
把B（-1，0）代入y=ax²+4ax+3得a=1，
∴抛物线是解析式为y=x²+4x+3．

 （2）如图1中，过E作EM⊥AB于M，作NK⊥EM于K．

∵∠K=∠EMG=∠NEG=90°，
∴∠NEK+∠ENK=90°，∠NEK+∠GEM=90°，
∴∠MEG=∠ENK，
在△ENK和△GEM中，
$\left\{\begin{array}{l}{∠K=∠EMG}\\{∠ENK=∠MEG}\\{EN=EG}\end{array}\right.$，
∴△ENK≌△GEM，
∴NK=EM，
∵OA=OC，∠AOC=90°，
∴∠EAM=∠AEM=45°，
∴NK=EM=AM，∵NK∥AM，
∴四边形ANKM是平行四边形，
∵∠AMK=90°，
∴四边形ANKM是矩形，
∴∠NAM=90°，
∵PG⊥AB，
∴∠PGA=∠PAM，
∴AN∥PG．

（3）如图2中，连接GN、GF，作EK⊥PC于K，FH⊥x轴于H．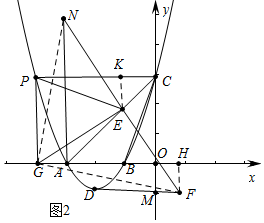

∵EG=EN=EF，GE⊥NF，
∴GN=GF，∠NGF=90°，
∵∠AGN+∠ANG=90°，∠AGN+∠FGH=90°，
∴∠ANG=∠FGH，
在△AGN和△HFG中，
$\left\{\begin{array}{l}{∠GAN=∠FHG}\\{∠ANG=∠FGH}\\{GN=GF}\end{array}\right.$，
∴△AGN≌△FHG，
∴AG=FH，
∵D（-2，-1），FM⊥y轴，FM经过点D，
∴FH=AG=1，
∴P（-4，3），∵OC=PG=3，PG∥OC，
∴四边形PGOC是平行四边形，
∵∠GOC=90°，
∴四边形PGOC是矩形，
∵∠EPC+90°=∠ABC=90°+∠BCO，
∴∠EPC=∠BCO，
∴tan∠EPC=tan∠BCO=$\frac{BO}{CO}$=$\frac{1}{3}$=$\frac{KE}{PK}$，
∴PK=3EK，
∵∠KCE=∠ECO=45°，
∴KE=KC，
∴PK=3KC，
∴KC=1，
∴E（-2，1）．

点评 本题考查二次函数综合题、全等三角形的判定和性质、矩形的判定和性质、锐角三角函数等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线构造全等三角形，属于中考压轴题．