
【题目】)如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF=![]() AD,求出点E的坐标.
AD,求出点E的坐标.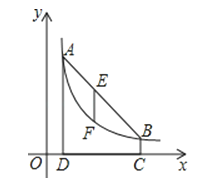
【答案】解:(1)设反比例函数的解析式为y=![]() ,
,
把(n,1)代入得:k=n,
即y=![]() ,
,
∵点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5,
∴![]() ,
,
解得:m=1,n=6,
即A(1,6),B(6,1);
反比例函数的解析式为:y=![]() ;
;
(2)设直线AB的解析式为y=ax+b,
把A(1,6)和B(6,1)代入得:![]()
解得:a=﹣1,b=7,
即直线AB的解析式为:y=﹣x+7,
设E点的横坐标为m,则E(m,﹣m+7),F(m,![]() ),
),
∴EF=﹣m+7﹣![]() ,
,
∵EF=![]() AD,
AD,
∴﹣m+7﹣![]() =
=![]() ,
,
解得:m=2,m2=3,
经检验都是原方程的解,
即E的坐标为(2,5)或(3,4).
【解析】(1)设反比例函数的解析式为y=![]() , 根据题意得出方程组
, 根据题意得出方程组![]() , 求出方程组的解即可;
, 求出方程组的解即可;
(2)设直线AB的解析式为y=ax+b,求出直线AB的解析式,设E点的横坐标为m,则E(m,﹣m+7),F(m,![]() ),求出EF=﹣m+7﹣
),求出EF=﹣m+7﹣![]() , 得出关于m的方程,求出m即可.
, 得出关于m的方程,求出m即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上有两点![]() ,
, ![]() ,点
,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() .
.
(![]() )如图
)如图![]() ,现有两动点
,现有两动点![]() ,
, ![]() 分别从
分别从![]() ,
, ![]() 出发同时向右运动,点
出发同时向右运动,点![]() 的速度是点
的速度是点![]() 的速度
的速度![]() 倍少
倍少![]() 个单位长度/秒,经过
个单位长度/秒,经过![]() 秒,点
秒,点![]() 追上点
追上点![]() ,求动点
,求动点![]() 的速度.
的速度.
(![]() )如图
)如图![]() ,
, ![]() 表示原点,动点
表示原点,动点![]() ,
, ![]() 分别从
分别从![]() ,
, ![]() 两点同时出发向左运动,同时动点
两点同时出发向左运动,同时动点![]() 从点
从点![]() 出发向右运动,点
出发向右运动,点![]() ,
, ![]() ,
, ![]() 的速度分别为
的速度分别为![]() 个单位长度/秒、
个单位长度/秒、![]() 个单位长度/秒、
个单位长度/秒、![]() 个单位长度/秒;如果点
个单位长度/秒;如果点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,试说明在运动过程中等量关系
的中点,试说明在运动过程中等量关系![]() 始终成立.
始终成立.
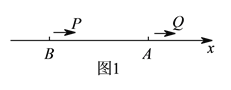
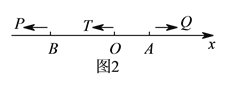
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式﹣2x﹣x3+2x2+5按降幂排列,正确的是( )
A.x3﹣2x+2x2+5
B.5﹣2x+2x2﹣x3
C.﹣x3+2x2+2x+5
D.﹣x3+2x2﹣2x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCO是正方形,已知点C的坐标为(![]() , 1),则点B的坐标为( )
, 1),则点B的坐标为( )
A.(![]() ﹣1,
﹣1,![]() +1)
+1)
B.(![]() ﹣1,1)
﹣1,1)
C.(1,![]() +1)
+1)
D.(![]() ﹣1,2)
﹣1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com