
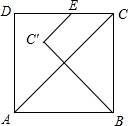
 如图所示,AB=4,AD=3,点E在CD上(不含端点C,D)的任一点,把△EBC沿BC折叠,当点C落在矩形ABCD的对角线上时,CE=$\frac{3}{2}$.
如图所示,AB=4,AD=3,点E在CD上(不含端点C,D)的任一点,把△EBC沿BC折叠,当点C落在矩形ABCD的对角线上时,CE=$\frac{3}{2}$. 分析 根据勾股定理得到BD=5,根据折叠的性质得到C′E=CE,BC′=BC=AD=3,求得C′D=2,∠DC′E=90°,根据勾股定理列方程即可得到结论.
解答 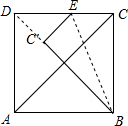 解:∵AB=4,AD=3,
解:∵AB=4,AD=3,
∴BD=5,
∵把△EBC沿BC折叠得到△BC′E,
∴C′E=CE,BC′=BC=AD=3,
∵当点C落在矩形ABCD的对角线上,
∴D,C′,B三点共线,
∴C′D=2,∠DC′E=90°,
∵DE=4-CE,
∵DE2=DC′2+C′E2,
即(4-CE)2=22+CE2,
∴CE=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,勾股定理,根据勾股定理列方程是解题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 地区 | 北京 | 广东 | 上海 | 浙江 | 福建 | 云南 | 湖北 |
| 同比涨幅(%) | 3.3 | 3.3 | 3 | 2.8 | 2.8 | 2.8 | 2.3 |
| A. | 2.8,2.8 | B. | 2.8,2.9 | C. | 3.3,2.8 | D. | 2.8,3.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.114×1011 | B. | 1.14×1010 | C. | 11.4×109 | D. | 114×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com