

分析 (1)根据矩形的性质易证,OA=OC,AB∥CD,根据AB∥CD,得到∠EAO=∠FCO,满足ASA可证;
(2)①先证△MOC∽△ACB,得MC:AC=OC:BC,计算MC,即可求出BM;
②若△BMO是等腰三角形,则可能BM=OM,OB=BM,OB=OM,分类讨论即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴OA=OC,AB∥CD,
∴∠EAO=∠FCO,
在△AOE和△COF中
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AEO=∠CFO}\end{array}\right.$,
∴△AOE≌△COF(AAS); 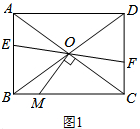
(2)①解:如图1,∵MO⊥AC,
∴∠MOC=90°,
∵∠ABC=90°,
∴∠MOC=∠ABC,
又∵∠MCO=∠MCO,
∴△MOC∽△ACB,
∴MC:AC=OC:BC,
∵AB=3,BC=4,
∴AC=5,
∴OC=2.5,
∴MC:5=2.5:4,
∴MC=$\frac{25}{8}$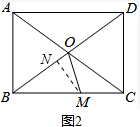 ,
,
∴BM=$\frac{7}{8}$;
②如图2,△BMO是等腰三角形时,有三种情况:
(Ⅰ)OB=OM,此时M与C重合,BM=4;
(Ⅱ)OB=BM,BM=OB=$\frac{1}{2}$BD=2.5;
(Ⅲ)BM=OM,作MN⊥BD,
∴BN=$\frac{1}{2}$B0=$\frac{5}{4}$;
∵△BMN∽△BDC
∴$\frac{BN}{BC}=\frac{BM}{BD}$,
∴BM=$\frac{BN•BD}{BC}$=$\frac{\frac{5}{4}×5}{4}$=$\frac{25}{16}$,
∴BM=2.5或4或$\frac{25}{16}$.
点评 本题主要考查了三角形全等的判定、相似三角形的判定与性质、等腰三角形的判定与性质,第3小题考查学生思维的全面性,恰当分类讨论是解决问题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )| A. | 4:5 | B. | 3:5 | C. | 4:9 | D. | 3:8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:| 年份 支出项目(单位:元) | 2010年 | 2012年 | 2014年 |
| 食品支出 | a | 5600 | 6300 |
| 医疗、保健支出 | 2000 | 2200 | 3000 |
| 家庭用品及服务支出 | 3300 | 4000 | 5700 |
| 其他支出 | 2500 | 4200 | 6000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
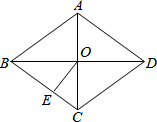 如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )
如图,菱形ABCD的面积为S,对角线交于点O,OE⊥BC于点E.下列结论正确的是( )| A. | S=AC•BD | B. | S=4BC•OE | C. | S=2AB•OE | D. | S=2BD•AO |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
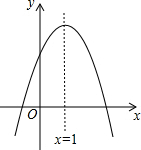 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
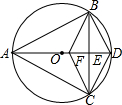 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 255分 | B. | 84分 | C. | 84.5分 | D. | 86分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com