
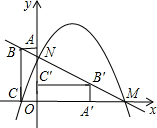
 如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:
如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:分析 (1)易得点B、点B′的坐标,然后运用待定系数法可求出直线BB′的解析式;
(2)由直线BB′的解析式从而求出点M、N的坐标,然后运用待定系数法就可求出抛物线的解析式;
(3)设OP与直线MN交于点H,过点P作PG⊥y轴于点G,如图2,运用等积法可求出OP的长,然后运用相似三角形的性质就可求出点P的坐标,然后把点P的坐标代入抛物线的解析式,就可解决问题.
解答 解:(1)由题意得,B(-1,3),B'(3,1)
∴直线BB'的解析式为$y=-\frac{1}{2}x+\frac{5}{2}$
(2)直线BB'与x轴的交点为M(5,0),与y轴的交点N(0,$\frac{5}{2}$),
设抛物线的解析式为y=a(x-5)(x+1),
∵抛物线过点N,∴$\frac{5}{2}=a×({-5})×1$,
∴$a=-\frac{1}{2}$,
∴抛物线的解析式为$y=-\frac{1}{2}({x-5})({x+1})$=$-\frac{1}{2}{x^2}+2x+\frac{5}{2}$;
(3)点P不在抛物线上.
理由如下:
如右图,设OP与直线MN交于点H,过点P作PG⊥y轴于点G,由题可得OP⊥MN,OP=2OH,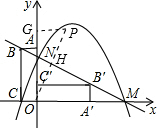
∴∠PGO=∠OHN=90°
在Rt△MON中,
∵OM=5,ON=$\frac{5}{2}$,
∴MN=$\sqrt{O{M}^{2}+O{N}^{2}}$=$\frac{5\sqrt{5}}{2}$
∴OH=$\frac{OM•ON}{MN}$=$\sqrt{5}$,
∴OP=2OH=2$\sqrt{5}$,
∵∠NOM=90°,∠OHN=90°,
∴∠NOH=90°-∠HOM=∠OMN.
又∵∠PGO=∠NOM=90°,
∴△PGO∽△NOM,
∴$\frac{PG}{ON}=\frac{OG}{MO}=\frac{OP}{MN}$,
∴$\frac{PG}{\frac{5}{2}}=\frac{OG}{5}=\frac{2\sqrt{5}}{\frac{5\sqrt{5}}{2}}=\frac{4}{5}$,
∴PG=2,OG=4,
∴点P的坐标为(2,4),
当x=2时,y=$\frac{9}{2}$≠4,
∴点P不在抛物线上.
点评 本题主要考查了用待定系数法求一次函数和二次函数的解析式,勾股定理,有一定综合性,但难度不大.运用面积法和相似三角形的性质是解决第(3)小题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
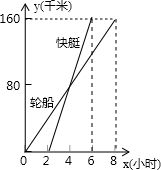 一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶路程随时间变化的图象如图,下列结论错误的是( )
一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶路程随时间变化的图象如图,下列结论错误的是( )| A. | 轮船的速度为20 km/h | B. | 快艇的速度为$\frac{80}{3}$ km/h | ||
| C. | 轮船比快艇先出发2 h | D. | 快艇比轮船早到2 h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
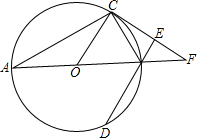 如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,过C作⊙O的切线交AB的延长线于点F,DB⊥CF,垂足为E.
如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,过C作⊙O的切线交AB的延长线于点F,DB⊥CF,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )
一汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线ABCDE),根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在行驶过程中的平均速度为$\frac{80}{3}$千米/小时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.其中正确的说法共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=ax2+bx+1经过A(1,3),B(2,1)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+1经过A(1,3),B(2,1)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com