
分析 设a-c=-2k,a+b=7k,c-b=k,于是得到a=7k-b,c=k+b,代入a-c=-2k和a+b+c=24,解方程组$\left\{\begin{array}{l}{8k-2b=0}\\{8k+b=24}\end{array}\right.$,得到k=2,b=8,求得a=6,c=10即可.
解答 解:设a-c=-2k,a+b=7k,c-b=k,
∴a=7k-b,c=k+b,
∴a-c=7k-b-k-b=-2k,
∵a+b+c=24,
∴7k-b+b+k+b=24,
∴$\left\{\begin{array}{l}{8k-2b=0}\\{8k+b=24}\end{array}\right.$,
解得:k=2,b=8,
∴a=6,c=10.
点评 本题考查了比例线段,因式分解的应用,熟练掌握比例线段的性质是解题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题
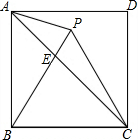 如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点P在正方形ABCD内,△PBC是正三角形,连接AP、AC,过点P作BC的垂线交AC于点E,若AP=1,则PE=$\frac{\sqrt{6}-\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com