
| A. | m≠1 | B. | m≥0 | C. | m≥0 且 m≠1 | D. | m为任意实数 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
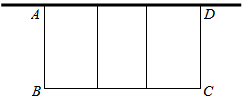 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有两道篱笆的长方形花圃ABCD.求长方形花圃ABCD面积s与AB的长x的函数关系式,并求出AB的长为何值时面积有最大值.
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有两道篱笆的长方形花圃ABCD.求长方形花圃ABCD面积s与AB的长x的函数关系式,并求出AB的长为何值时面积有最大值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察流花河的水文资料(单位:米),完成下列问题
观察流花河的水文资料(单位:米),完成下列问题| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位变化/米 | +0.2 | +0.81 | -0.35 | +0.03 | +0.28 | -0.36 | -0.01 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,D、E、F分别为AB、BC、AC上的点,且BD=CE,∠DEF=∠B.
如图,△ABC中,AB=AC,D、E、F分别为AB、BC、AC上的点,且BD=CE,∠DEF=∠B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com