
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的对称轴是直线
的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)点![]() ,
, ![]() 在抛物线上,若
在抛物线上,若![]() ,请直接写出
,请直接写出![]() 的取值范围;
的取值范围;
(3)设点![]() 为抛物线上的一个动点,当
为抛物线上的一个动点,当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的上方,求
的上方,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:(1)由抛物线的对称轴方程可求得m=1,从而可求得抛物线的表达式;
(2)将x=3代入抛物线的解析式,可求得y2=3,将y=3代入抛物线的解析式可求得x1=-1,x2=3,由抛物线的开口向下,可知当n<-1或n>3时,y1<y2;
(3)先根据题意画出点M关于y轴对称点M′的轨迹,然后根据点M关于y轴的对称点都在直线y=kx-4的上方,求出最大与最小两个关于k的方程,即可求得k的取值范围.
解:(1)∵抛物线的对称轴是![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)将x=3代入抛物线的解析式得y=32+2×3=3,
将y=3代入得:x2+2x=3,
解得:x1=1,x2=3.
∵a=1<0,
∴当n<1或n>3时,y1<y2.
(3) 由题意得抛物线![]() ,
,
关于![]() 轴对称的抛物线为
轴对称的抛物线为![]() .,
.,
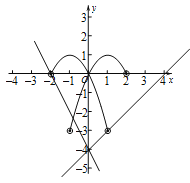
当![]() ,
,
当直线![]() 经过点
经过点![]() 时,
时,
可得![]() ;
;
当![]() ,
,
当直线![]() 经过点
经过点![]() 时,
时,
可得![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=![]() (BC+BF).
(BC+BF).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2=![]() 的图象相交于A,B两点,点B的坐标为(2m,-m).
的图象相交于A,B两点,点B的坐标为(2m,-m).
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.
(1)求证:△ABE≌△DBC.

接着张老师又让学生分小组进行探究:你还能得出什么结论?
精英小组探究的结论是:AM=DN.
奋斗小组探究的结论是:△EMB≌△CNB.
创新小组探究的结论是:MN∥AC.
(2)你认为哪一小组探究的结论是正确的?
(3)选择其中你认为正确的一种情形加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com