Question

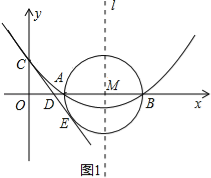
【题目】（12分）如图，已知抛物线（）的顶点坐标为（4， ），且与y轴交于点C（0，2），与x轴交于A、B两点（点A在点B的左边）.

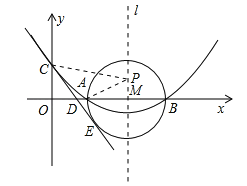
（1）求抛物线的解析式及A、B两点的坐标；

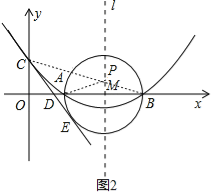
（2）在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小，若存在，求AP+CP的最小值；若不存在，请说明理由；

（3）在以AB为直径的⊙M中，CE与⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．

Answer 1

【答案】（1），A（2，0）B（6，0）；（2）存在， ；（3）．

【解析】试题分析：（1）利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标；

（2）线段BC的长即为AP+CP的最小值；

（3）连接ME，根据CE是⊙M的切线得到ME⊥CE，∠CEM=90°，从而证得△COD≌△MED，设OD=x，在RT△COD中，利用勾股定理求得x的值即可求得点D的坐标，然后利用待定系数法确定线段CE的解析式即可．

试题解析：（1）由题意，设抛物线的解析式为（），∵抛物线经过（0，2），∴，解得： ，∴，即： ，当时， ，解得： 或，∴A（2，0），B（6，0）；

（2）存在，如图2，由（1）知：抛物线的对称轴l为x=4，因为A、B两点关于l对称，连接CB交l于点P，则AP=BP，所以AP+CP=BC的值最小．∵B（6，0），C（0，2），∴OB=6，OC=2，∴BC=，∴AP+CP=BC=，∴AP+CP的最小值为；

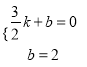（3）如图3，连接ME，∵CE是⊙M的切线，∴ME⊥CE，∠CEM=90°，∵C的坐标（0，2），∴OC=2，∵AB=4，∴ME=2，∴OC=ME=2，∵∠ODC=∠MDE，在△COD与△MED中，∵∠COD=∠MED，∠ODC=∠EDM，OC=ME，∴△COD≌△MED（AAS），∴OD=DE，DC=DM，设OD=x，则CD=DM=OM﹣OD=4﹣x，则Rt△COD中， 2，∴，∴，∴D（，0），设直线CE的解析式为（），∵直线CE过C（0，2），D（，0）两点，则，解得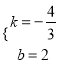： ，∴直线CE的解析式为．