
【题目】如图,已知抛物线y=![]() (x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.

【答案】(1)点C(0,﹣![]() ) (2)﹣
) (2)﹣![]() (3)(﹣4,2
(3)(﹣4,2![]() )或(6,2
)或(6,2![]() )或(0,﹣
)或(0,﹣![]() )
)
【解析】(1)令y=0可求得点A、点B的横坐标,令x=0可求得点C的纵坐标;
(2)根据两点之间线段最短作M点关于直线x=﹣2的对称点M′,当N(﹣2,N)在直线M′B上时,MN+BN的值最小;
(3)需要分类讨论:△PAB∽△ABD、△PAB∽△ABD,根据相似三角形的性质求得PB的长度,然后可求得点P的坐标.
解:(1)令y=0得x1=﹣2,x2=4,
∴点A(﹣2,0)、B(4,0)
令x=0得y=﹣![]() ,
,
∴点C(0,﹣![]() )
)
(2)将x=1代入抛物线的解析式得y=﹣![]()
∴点M的坐标为(1,﹣![]() )
)
∴点M关于直线x=﹣2的对称点M′的坐标为(﹣5,![]() )
)
设直线M′B的解析式为y=kx+b
将点M′、B的坐标代入得: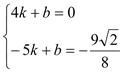
解得: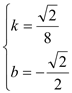
所以直线M′B的解析式为y=![]() ×
×![]() .
.
将x=﹣2代入得:y=﹣![]() ,
,
所以n=﹣![]() .
.
(3)过点D作DE⊥BA,垂足为E.
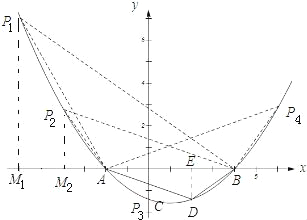

由勾股定理得:
AD=![]() =
=![]() =3
=3![]() ,
,
BD=![]() =
=![]() =
=![]() ,
,
如下图,①当P1AB∽△ADB时,
![]() =
=![]() 即:
即:![]() =
=![]() ,
,
∴P1B=6![]()
过点P1作P1M1⊥AB,垂足为M1.
∴![]() =
=![]() 即:
即:![]() =
=![]()
解得:P1M1=6![]() ,
,
∵![]() =
=![]() 即:
即:![]() =
=![]()
解得:BM1=12
∴点P1的坐标为(﹣8,6![]() )
)
∵点P1不在抛物线上,所以此种情况不存在;
②当△P2AB∽△BDA时,![]() =
=![]() 即:
即:![]() =
=![]()
∴P2B=6![]() ,
,
过点P2作P2M2⊥AB,垂足为M2.
∴![]() =
=![]() ,即:
,即:![]() =
=![]()
∴P2M2=2![]() ,
,
∵![]() =
=![]() ,即:
,即:![]() =
=![]()
∴M2B=8
∴点P2的坐标为(﹣4,2![]() )
)
将x=﹣4代入抛物线的解析式得:y=2![]() ,
,
∴点P2在抛物线上.
由抛物线的对称性可知:点P2与点P4关于直线x=1对称,
∴P4的坐标为(6,2![]() ),
),
当点P3位于点C处时,两三角形全等,所以点P3的坐标为(0,﹣![]() ),
),
综上所述点P的坐标为:(﹣4,2![]() )或(6,2
)或(6,2![]() )或(0,﹣
)或(0,﹣![]() )时,以P、A、B为顶点的三角形与△ABD相似.
)时,以P、A、B为顶点的三角形与△ABD相似.
“点睛”本题综合考查了二次函数、一次函数、轴对称…路径最短、相似三角形的性质,难度较大,利用相似三角形的性质求得PB的长是解题的关键,解答本题需要注意的是在不确定相似三角形的对应角和对应边的情况下分类讨论,不要漏解.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+3的图象与x轴,y轴交于A,B两点,与反比例函数![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
①△CEF与△DEF的面积相等;
②△AOB∽△FOE;
③△DCE≌△CDF;
④AC=BD.
其中正确的结论是( )

A. ①② B. ①②③ C. ①②③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值;
(2)补全条形统计图;
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适宜采用普查方式的是( )
A.对全国初中学生视力状况的调査
B.对“十一国庆”期间全国居民旅游出行方式的调查
C.旅客上飞机前的安全检查
D.了解某种品牌手机电池的使用寿命
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com