
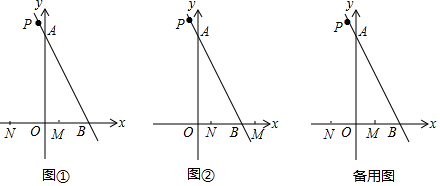
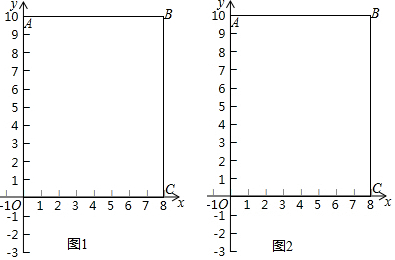
���� ��1�������A��B�������꣬���tan��ABO��ֵ�����ɽ�����⣮����PMN�ǵȱ�������ʱ���������������۵�M��λ�ü��ɣ�
��2�����������λ���ͼ�μ��ɣ�
��3����ͼ���У������O�侭����M��N��������ֱ��AB���У��е�ΪP����MPN=30�㣬����O��M��O��N��O��P����OG��PN��G��PH��OB��H����취�����M��λ�ã��ٸ��ݶԳ���ȷ����M��ֱ��AB�Ҳ��λ�ü��ɽ�����⣮
��� �⣺��1������ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��
��x=0��y=2$\sqrt{3}$����y=0��x=2��
��A��0��2$\sqrt{3}$����B��2��0����
��OA=2$\sqrt{3}$��OB=2��
��tan��ABO=$\frac{OA}{OB}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$��
���ABO=60�㣬
��ͼ���У���M��B�غ�ʱ����PMN�����ǵȱ������Σ���ʱa=2��
����N��B�غ�ʱ����PMN�����ǵȱ������Σ���ʱa=2+$\sqrt{3}$��
�൱��MPNΪ�ȱ�������ʱ��a��ֵ��2��2+$\sqrt{3}$��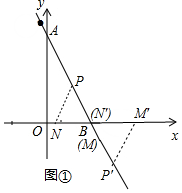
�ʴ𰸷ֱ�Ϊ60��2��2+$\sqrt{3}$��
��2�����������ĵ�P��ͼ��ʾ��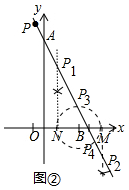 ��
��
��3����ͼ���У������O�侭����M��N��������ֱ��AB���У��е�ΪP����MPN=30�㣬����O��M��O��N��O��P����OG��PN��G��PH��OB��H��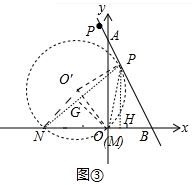
�ߡ�MO��N=2��MPN=60�㣬O��N=O��M��
���O��MN�ǵȱ������Σ�
��O��P=O��M=O��N=MN=$\sqrt{3}$����O��MN=��ABO=60�㣬
��AB��O��M��
��O��P��AB��
��O��P��O��M��
���PO��M=90�䣬
��PM=$\sqrt{2}$O��P=$\sqrt{6}$��
���PNM=$\frac{1}{2}$��PO��M=45�㣬
��GN=GM=$\frac{\sqrt{6}}{2}$��PG=$\sqrt{3}$GM=$\frac{3\sqrt{2}}{2}$��
��PN=$\frac{\sqrt{6}+3\sqrt{2}}{2}$��
��NH=PH=$\frac{\sqrt{3}+3}{2}$��BH=$\frac{1+\sqrt{3}}{2}$��
��NB=NH+BH=2+$\sqrt{3}$��
��BM=BN=MN=2+$\sqrt{3}$-$\sqrt{3}$=2��
���M���O�غϣ���ʱa=0��
����O����ֱ��AB�Ҳ�ʱ��ͬ���ɵ�BN=2��OM=4+$\sqrt{3}$����ʱa=4+$\sqrt{3}$��
�൱��MPN=30��ʱ����a��ȡֵ��Χ0��a��4+$\sqrt{3}$��
�ʴ�Ϊ0��a��4+$\sqrt{3}$��
���� ���⿼��һ�κ����ۺ��⡢�ȱ������ε����ʡ�ֱ�������ε��ж������ʡ�ֱ����Բ��λ�ù�ϵ��֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ����츨��Բ������⣬�����п�ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
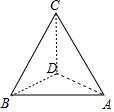 ��ͼ��Ϊ�˹���ij���ĸ߶ȣ���ͬһˮƽ���A��B���㴦���в������ڵ�A���������C����ƫ��20��ķ����ϣ�����Ϊ60�㣻�ڵ�B���������C�ڶ�ƫ��40��ķ����ϣ�����Ϊ30�㣬��A��B�������130m�������ĸ߶�CD=10$\sqrt{39}$m��
��ͼ��Ϊ�˹���ij���ĸ߶ȣ���ͬһˮƽ���A��B���㴦���в������ڵ�A���������C����ƫ��20��ķ����ϣ�����Ϊ60�㣻�ڵ�B���������C�ڶ�ƫ��40��ķ����ϣ�����Ϊ30�㣬��A��B�������130m�������ĸ߶�CD=10$\sqrt{39}$m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{����3��^{2}}$=��3 | B�� | 23��24=27 | C�� | -2a2•3a=6a3 | D�� | 3m2�£�3m-1��=m-3m2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com