
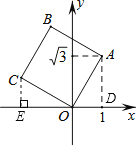
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,![]() ),则点C的坐标为( )
),则点C的坐标为( )

A. (![]() ,-1)B. (-1,
,-1)B. (-1,![]() )C. (
)C. (![]() ,1)D. (-
,1)D. (-![]() ,1)
,1)
【答案】D
【解析】
过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD和△OCE全等,根据全等三角形对应边相等可得OE=AD,CE=OD,然后根据点C在第二象限写出坐标即可.
如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
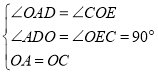 ,
,
∴△AOD≌△OCE(AAS),
∴OE=AD=![]() ,CE=OD=1,
,CE=OD=1,
∵点C在第二象限,
∴点C的坐标为(-![]() ,1).
,1).
故选:D.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
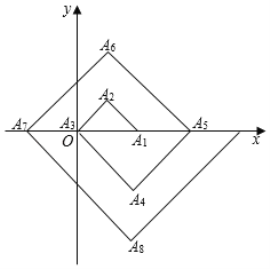
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
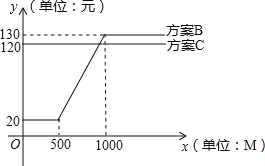
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
科目:初中数学 来源: 题型:
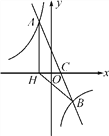
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC是等腰锐角三角形,AB=AC(![]() ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
(2)如图2,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
(3)如图3,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数(如有需要,可在答题卡相应位置另外画图).

查看答案和解析>>
科目:初中数学 来源: 题型:
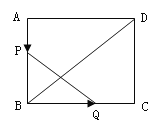
【题目】如图,已知矩形![]() ,长
,长![]() ,宽
,宽![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上运动的两点。若
上运动的两点。若![]() 自点
自点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向运动,同时,
方向运动,同时, ![]() 自点
自点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,则经过____________秒,以
方向运动,则经过____________秒,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似。
相似。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.

(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() (k≠0)的图象经过
(k≠0)的图象经过![]() ,
, ![]() 两点,二次函数
两点,二次函数![]() (其中a>2).
(其中a>2).

(1)求一次函数的表达式及二次函数图象的顶点坐标(用含a的代数式表示);
(2)利用函数图象解决下列问题:
①若![]() ,求当
,求当![]() 且
且![]() ≤0时,自变量x的取值范围;
≤0时,自变量x的取值范围;
②如果满足![]() 且
且![]() ≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.
≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com