
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC= ![]() ,D、E是AB边上的两个动点,满足∠DCE=45°.
,D、E是AB边上的两个动点,满足∠DCE=45°. 
(1)如图②,把△ADC绕着点C顺时针旋转90°,得到△BKC,连结EK. 
①求证:△DCE≌△KCE.
②求证:DE2=AD2+BE2 .
③思考与探究:当点D从点A向AB的中点运动的过程中,请尝试写出DE长度的变化趋势 ![]() ;并直接写出DE长度的最大值或最小值
;并直接写出DE长度的最大值或最小值 ![]() (标明最大值或最小值).
(标明最大值或最小值).
(2)如图③,若△CDE的外接圆⊙O分别交AC,BC于点F、G,求证:CF:CG=BE:AD. 
【答案】
(1)证明:①如图1,由旋转得:△ACD≌△BCK,
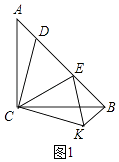
∴CD=CK,∠ACD=∠BCK,
∵∠DCE=45°,∠ACB=90°,
∴∠ACD+∠BCE=90°﹣45°=45°,
∴∠BCK+∠BCE=45°,
即∠KCE=45°,
∴∠KCE=∠DCE,
∵CE=CE,
∴△DCE≌△KCE(SAS);
②如图2,∵△ABC是等腰直角三角形,
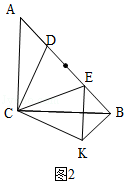
∴∠A=∠ABC=45°,
∵△DCE≌△KCE,
∴DE=EK,∠KBC=∠A=45°,KB=AD,
∴∠KBE=45°+45°=90°,
在Rt△KBE中,KE2=BE2+KB2,
∴DE2=AD2+BE2;|当D从A到D时,DE越来越小,再继续运动到中点时,越来越大;|DE最大值=1,DE最小值=2 ![]() ﹣2
﹣2
③∵∠ACB=90°,AC=BC= ![]() ,
,
∴AB= ![]() =2,
=2,
设AD=x,DE=y,则BE=2﹣x﹣y,
当点D从点A向AB的中点运动的过程中,0≤y≤1,0≤x≤1,AD=BE时,DE最小,如图2,BE=BK=x,
则x=2﹣x﹣y,
y=2﹣2x,
∵KE2=BE2+KB2,
∴y2=x2+x2,
(2﹣2x)2=2x2,
x2﹣4x+2=0,
解得:x1=2+ ![]() (不符合题意,舍去),x2=2﹣
(不符合题意,舍去),x2=2﹣ ![]() ,
,
∴y=2﹣2(2﹣ ![]() )=2
)=2 ![]() ﹣2,
﹣2,
即DE的最小值是:2 ![]() ﹣2,
﹣2,
当D与A重合或D与AB的中点重合时,DE最大,最大值是1;
∴DE长度的变化趋势是:当D从A到D时,DE越来越小,再继续运动到中点时,越来越大;
故答案为:当D从A到D时,DE越来越小,再继续运动到中点时,越来越大;DE最大值=1, ![]() ;
;
(2)如图3,把△ADC绕着点C顺时针旋转90°,得到△BKC,连结EK,EG,
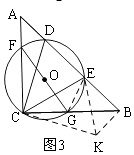
∵D、C、E、G四点共圆,
∴∠EGB=∠CDE,
∵∠DCE=∠EBC=45°,
在△CDE和△GEB中,∴∠CED=∠GEB,
由①得:△CDE≌△CKE,
∴∠CED=∠CEK,
∴∠CEK=∠GEB,
∴∠CEK﹣∠GEK=∠GEB﹣∠GEK,
即∠CEG=∠KEB,
∵∠CEG=∠CFG,
∴∠CFG=∠KEB,
∵∠ACB=∠EBK=90°,
∴△FCG∽△EBK,
∴ ![]() ,
,
由①得:△ACD≌△BCK,
∴AD=BK,
∴CF:CG=BE:AD.
【解析】(1)①由旋转得:CD=CK,∠ACD=∠BCK,证明∠KCE=∠DCE=45°,根据SAS证明:△DCE≌△KCE;②先求∠KBE=45°+45°=90°,在Rt△KBE中,利用勾股定理可得结论;③如图2,本题可以看作是周长一定,即直角△EBK的周长为2,斜边DE的变化趋势,发现根据直角三角形斜边中线等于斜边的一半可知:DE的大小取决于直角△EBK斜边中线的大小,当直角△EBK是等腰直角三角形(设两直角边分别为a、b时,斜边为 ![]() ,因为a2+b2≥2ab,当a=b时,
,因为a2+b2≥2ab,当a=b时, ![]() 有最小值)时,中线最短,由此计算DE的最小值,当D与A重合或D与AB的中点重合时,DE最大,最大值是1;(2)如图3,同①作辅助线,证明△FCG∽△EBK,列比例式得
有最小值)时,中线最短,由此计算DE的最小值,当D与A重合或D与AB的中点重合时,DE最大,最大值是1;(2)如图3,同①作辅助线,证明△FCG∽△EBK,列比例式得 ![]() ,由①得:△ACD≌△BCK, AD=BK,所以CF:CG=BE:AD.
,由①得:△ACD≌△BCK, AD=BK,所以CF:CG=BE:AD.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y= ![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( ) 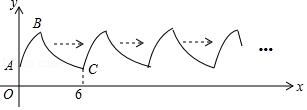
A.72
B.36
C.16
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B. 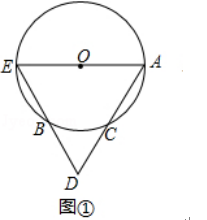
(1)求证:点C是劣弧 ![]() 的中点;
的中点;
(2)如图②,连结EC,若AE=2AC=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个矩形的两邻边之比为 ![]() ,则称该矩形为“特比矩形”.
,则称该矩形为“特比矩形”.
(1)如图①,在“特比矩形”ABCD中, ![]() =
= ![]() ,求∠AOD的度数;
,求∠AOD的度数; 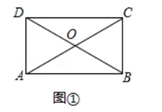
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB= ![]() ,求矩形CDEF的面积;
,求矩形CDEF的面积; 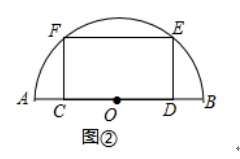
(3)在平面直角坐标系xOy中,⊙O的半径为 ![]() ,点Q的坐标为(q,2
,点Q的坐标为(q,2 ![]() ),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 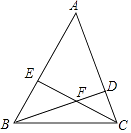
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
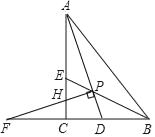
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角三角形ABC中,边AC长4cm,边BC长3cm,边AB长5cm.
(1)三角形绕着边AC旋转一周,所得几何体的体积和绕着边BC旋转一周所得几何体体积是否一样?通过计算说明;
(2)若绕着边AB旋转一周,所得的几何体的体积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察,在如图所示的各图中找对顶角(不含平角):

(1)如图a,图中共有_____对对顶角.
(2)如图b,图中共有_____对对顶角.
(3)如图c,图中共有_____对对顶角
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?
(5)若有2000条直线相交于一点,则可形成多少对对顶角?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com