(1)证明:∵△ABD和△DCE都是等边三角形,
∴∠ADB=∠CDE=60°,AD=BD,CD=DE.
∴∠ADB+∠BDC=∠BDC+∠FDE,即∠ADC=∠BDE.
∴△ADC≌△BDE.
∴AC=BE.
(2)解:∵△DCE是等边三角形,
∴DE=CE,又BE⊥DC,
∴F为DC的中点(三线合一),
∴BE是CD的中垂线.
∴DB=CB.又△ABD是等边三角形,
∴AB=DB=BC,
∴△ADC是直角三角形(三角形一边上的中线等于这边的一半,则这边所对的角为直角),
∵∠A=60,
∴∠BDC=∠ACD=90°-∠A=90°-60°=30°.
分析:(1)由等量加上等量还是等量知,∠ADC=∠BDE,由等边三角形的性质知,AD=BD,CD=DE,故由SAS证得△ADC≌△BDE,可得AC=BE
(2)由题意知,BE是CD的中垂线,由中垂线的性质:中垂线上的点到线段的两个端点的距离相等知,DE=BC=AB,故△ADC是直角三角形,点B是斜边上的中点则可求得∠BDC的度数.
点评:本题考查了等边三角形的性质、全等三角形的判定和性质、中垂线的判定和性质及直角三角形的判定和性质求解.各种知识的综合运用是正确解答本题的关键.

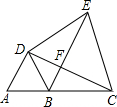
 已知如图,B是AC上一点,△ABD和△DCE都是等边三角形.
已知如图,B是AC上一点,△ABD和△DCE都是等边三角形.


 阅读快车系列答案
阅读快车系列答案