
分析 (1)先根据题意得出xy的值,再代入代数式进行计算即可;
(2)根据分式混合运算的法则把原式进行化简,再选出合适的x的值代入进行计算即可.
解答 解:(1)∵x+y=15,x2+y2=113,
∴(x+y)2=225,即x2+y2+2xy=225,
∴2xy=225-113=112,
∴xy=56,
∴x2-xy+y2=113-56=57;
(2)原式=$\frac{(x-2)^{2}}{2x}$•$\frac{x}{x-2}$+1
=$\frac{x-2}{2}$+1
=$\frac{x}{2}$,
当x=1时,原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.


科目:初中数学 来源: 题型:选择题
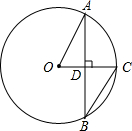 如图,⊙O的弦AB垂直半径OC于点D,∠CBA=30°,OC=2cm,则弦AB的长为( )
如图,⊙O的弦AB垂直半径OC于点D,∠CBA=30°,OC=2cm,则弦AB的长为( )| A. | 9cm | B. | 2$\sqrt{3}$cm | C. | $\frac{9}{2}$ cm | D. | $\frac{3\sqrt{3}}{2}$ cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
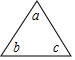 =a+b-c;$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.
=a+b-c;$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.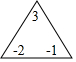
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|a|=-a,则a<0 | B. | 式子3xy2-4x3y+12是七次三项式 | ||
| C. | 若a<0,ab<0,则b>0 | D. | 若a=b,m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{8}$ | B. | $\frac{8}{9}$ | C. | -$\frac{8}{9}$ | D. | -$\frac{9}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
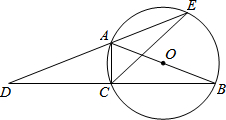 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com