
【题目】如图,四边形ABCD内接于⊙O.AC为直径,AC、BD交于E,![]() =
=![]() .
.
(1)求证:AD+CD=![]() BD;
BD;
(2)过B作AD的平行线,交AC于F,求证:EA2+CF2=EF2;
(3)在(2)条件下过E,F分别作AB、BC的垂线垂足分别为G、H,连GH、BO交于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O半径.
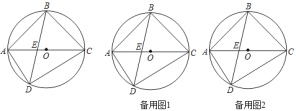
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)延长DA至W,使AW=CD,连接WB,证△BCD和△BAW全等,得到△WBD是等腰直角三角形,然后推出结论;
(2)过B作BE的垂线BN,使BN=BE,连接NC,分别证△AEB和△CNB全等,△BFE和△BFN全等,将EA,CF,EF三条线段转化为直角三角形的三边,即可推出结论;
(3)延长GE,HF交于K,通过大量的面积法的运用,将AE,CF,EF三条线段用含相同的字母表示出来,再根据第二问的结论求出相关字母的值,再求出AB的值,进一步求出⊙O半径.
解:(1)延长DA至W,使AW=CD,连接WB,
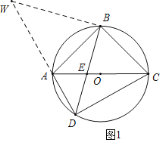
∵![]() =
=![]() ,
,
∴∠ADB=∠CDB=45°,AB=BC,
∵四边形ABCD内接于⊙O.
∴∠BAD+∠BCD=180°,
∵∠BAD+∠WAB=180°,
∴∠BCD=∠WAB,
在△BCD和△BAW中,
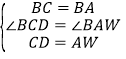 ,
,
∴△BCD≌△BAW(SAS),
∴BW=BD,∠BWA=∠ADB=45°,
∴△WBD是等腰直角三角形,
∴AD+DC=DW=![]() BD;
BD;
(2)如图2,设∠ABE=α,∠CBF=β,则α+β=45°,
过B作BE的垂线BN,使BN=BE,连接NC,
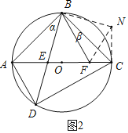
在△AEB和△CNB中,
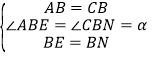 ,
,
∴△AEB≌△CNB(SAS),
∴AE=CN,
∠BCN=∠BAE=45°,
∴∠FCN=90°,
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN,
∴EF=FN,
∵在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
(3)如图3,延长GE,HF交于K,
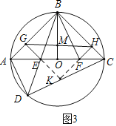
由(2)得EA2+CF2=EF2,
∴![]() EA2+
EA2+![]() CF2=
CF2=![]() EF2,
EF2,
∴S△AGE+S△CFH=S△EFK,
∴S△AGE+S△CFH+S五边形BGEFH=S△EFK+S五边形BGEFH,
即S△ABC=S矩形BGKH,
∴![]() S△ABC=
S△ABC=![]() S矩形BGKH,
S矩形BGKH,
∴S△GBH=S△ABO=S△CBO,
∴S△BGM=S四边形COMH,S△BMH=S四边形AGMO,
∵S四边形AGMO:S四边形COMH=8:9,
∴S△BMH:S△BGM=8:9,
∵BM平分∠GBH,
∴BG:BH=9:8,
设BG=9k,BH=8k,
∴CH=3+k,
∴AE=3![]() ,CF=
,CF=![]() (k+3),EF=
(k+3),EF=![]() (8k-3),
(8k-3),
∴(3![]() )2+[
)2+[![]() (k+3)]2=[
(k+3)]2=[![]() (8k-3)]2,
(8k-3)]2,
整理,得7k2-6k-1=0,
解得:k1=-![]() (舍去),k2=1,
(舍去),k2=1,
∴AB=12,
∴AO=![]() AB=6
AB=6![]() ,
,
∴⊙O半径为6![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt⊿ABC中,∠C = 90,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=6,OC=![]() ,则直角边BC的长为___________
,则直角边BC的长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:
.下列结论:
①△ADE∽△ACD; ②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8; ④0<CE≤6.4.

其中正确的结论是____________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A(﹣2,2)和点B(﹣3,﹣2)的位置如图所示.
(1)作出线段AB关于y轴对称的线段A′B′,并写出点A、B的对称点A′、B′的坐标;
(2)连接AA′和BB′,请在图中画一条线段,将图中的四边形AA′B′B分成两个图形,其中一个是轴对称图形,另一个是中心对称图形,并且线段的一个端点为四边形的顶点,另一个端点在四边形一边的格点上.(每个小正方形的顶点均为格点).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)从袋中一次摸出两个球,请用画树状图或列表格的方法列出所有等可能的结果,并求出摸到两个不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
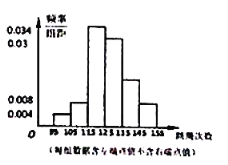
【题目】某校九年级学生共![]() 人,为了解这个年级学生的体能,从中抽取
人,为了解这个年级学生的体能,从中抽取![]() 名学生进行
名学生进行![]() 分钟的跳绳测试,结果统计的频率分布如图所示,其中从左至右前四个小长方形的高依次为
分钟的跳绳测试,结果统计的频率分布如图所示,其中从左至右前四个小长方形的高依次为![]()
![]() ,如果跳绳次数不少于
,如果跳绳次数不少于![]() 次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为__________.
次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com