练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    小强与小刚两位同学在学习“概率”时，做抛骰子(均匀立方体形状)试验，他们共抛了54次，出现不同向上点数的次数如下表：

    向上点数

    1

    2

    3

    4

    5

    6

    出现次数

    6

    9

    5

    8

    16

    10

    (1)请计算出现向上点数为3的频率及出现向上点数为5的频率.

    (2)小强说：“根据试验，一次试验中出现向上点数为5的概率最大.”小刚说：“如果抛540次，那么出现向上点数为6的次数正好是100次.”请判断小强和小刚说法的对错.

    (3)如果小强与小刚各抛一枚骰子，求出现向上点数之和为3的倍数的概率.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年初中毕业升学考试（山东潍坊卷）数学（解析版） 题型：填空题

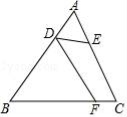
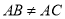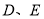    如图，在中，，分别为边、AC上的点，，,点为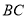边上一点，添加一个条件: ，可以使得与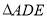相似.（只需写出一个）

    查看答案和解析>>

    科目：初中数学 来源：云南昆明市 2017年九年级数学中考模拟试卷（含答案） 题型：解答题

    请你根据王老师所给的内容，完成下列各小题：

    (1)如果x=-5,2⊙4=-18，求y的值；

    (2)若1⊙1=8，4⊙2=20，求x，y的值.

    查看答案和解析>>

    科目：初中数学 来源：九年级数学（浙教版）上册同步练习：1.3 二次函数的性质 题型：解答题

    如图，抛物线y＝ax2＋bx＋c经过△ABC的三个顶点，与y轴相交于(0， )，点A坐标为(－1，2)，点B是点A关于y轴的对称点，点C在x轴的正半轴上．

    （1）求该抛物线的函数解析式；

    （2）点F为线段AC上一动点，过点F作FE⊥x轴，FG⊥y轴，垂足分别为点E，G，当四边形OEFG为正方形时，求出点F的坐标；

    （3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：九年级数学（浙教版）上册同步练习：1.3 二次函数的性质 题型：单选题

    已知二次函数y＝ax2＋bx＋c，其自变量x与函数y的对应值如下表：

    x

    …

    －5

    －4

    －3

    －2

    －1

    0

    …

    y

    …

    4

    0

    －2

    －2

    0

    4

    …

    则下列说法正确的是( )

    A. 抛物线的开口向下 B. 当x＞－3时，y随x的增大而增大

    C. 二次函数的最小值是－2 D. 抛物线的对称轴是直线x＝－.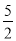

    查看答案和解析>>

    科目：初中数学 来源：九年级数学（浙教版）上册同步练习：2.3 用频率估计概率 题型：填空题

    某种油菜籽在相同条件下发芽试验的结果如下表：

    每批粒数n

    100

    300

    400

    600

    1000

    2000

    3000

    发芽的频数m

    96

    284

    384

    571

    948

    1902

    2848

    发芽的频

    0.960

    0.947

    0.960

    0.952

    0.948

    0.951

    0.949

    那么这种油菜籽发芽的概率约为___(结果精确到0.01).

    查看答案和解析>>

    科目：初中数学 来源：重庆合川区清平中学 2017年九年级数学中考模拟试卷（含答案） 题型：解答题

    某超市超市准备购进A、B两种品牌的书包共100个，已知两种书包的进价如下表所示，设购进A种书包x个，且所购进的两种书包能全部卖出，获得的总利润为y元．

    品牌

    购买个数（个）

    进价（元/个）

    售价（元/个）

    获利（元）

    A

    x

    50

    60

    __________

    B

    __________

    40

    55

    __________

    （1）将表格的信息填写完整；

    （2）求y关于x的函数表达式；

    （3）如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍，那么超市如何进货才能获利最大？并求出最大利润．

    查看答案和解析>>

    科目：初中数学 来源：重庆合川区清平中学 2017年九年级数学中考模拟试卷（含答案） 题型：单选题

    下列各组图形相似的是( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：江苏省2016-2017学年八年级5月单元测试数学试卷 题型：解答题

    知识迁移:我们知道，一次函数y=a（x﹣m）+n（a≠0，m＞0，n＞0）的图象是由一次函数y=ax的图象向右平移m个单位，再向上平移n个单位得到；类似地，函数y= +n（k≠0，m＞0，n＞0）的图象是由反比例函数的图象向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）．

    理解应用:(1)函数y=+1的图象可由函数y=的图象向右平移　 个单位，再向上平移　 个单位得到，其对称中心坐标为　 　．

    灵活应用:(2)如图，在平面直角坐标系xOy中，请根据所给的y=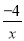的图象画出函数y=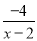﹣2的图象，并根据该图象指出，当x在　 　 时，y≥﹣1？

    实际应用:

    某老师对一位学生的学习情况进行跟踪研究，假设刚学完新知识时的记忆存留量为1，新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为y1=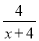；若在x=t（t≥4）时进行第一次复习，发现他复习后的记忆存留量是复习前的2倍（复习的时间忽略不计），且复习后的记忆存留量随x变化的函数关系为y2=，如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？

    查看答案和解析>>

    同步练习册答案