
ΓΨΧβΡΩΓΩ“―÷ΣΤΫΟφΆΦ–Έ![]() Θ§Βψ
Θ§Βψ![]() ΓΔ
ΓΔ![]() «
«![]() …œ»Έ“βΝΫΒψΘ§Έ“Ο«Α―œΏΕΈ
…œ»Έ“βΝΫΒψΘ§Έ“Ο«Α―œΏΕΈ![]() ΒΡ≥ΛΕ»ΒΡΉν¥σ÷Β≥ΤΈΣΤΫΟφΆΦ–Έ
ΒΡ≥ΛΕ»ΒΡΉν¥σ÷Β≥ΤΈΣΤΫΟφΆΦ–Έ![]() ΒΡΓΑΩμΨύΓ±Θ°άΐ»γΘ§’ΐΖΫ–ΈΒΡΩμΨύΒ»”ΎΥϋΒΡΕ‘Ϋ«œΏΒΡ≥ΛΕ»Θ°
ΒΡΓΑΩμΨύΓ±Θ°άΐ»γΘ§’ΐΖΫ–ΈΒΡΩμΨύΒ»”ΎΥϋΒΡΕ‘Ϋ«œΏΒΡ≥ΛΕ»Θ°
Θ®1Θ©–¥≥ωœ¬Ν–ΆΦ–ΈΒΡΩμΨύΘΚ
ΔΌΑκΨΕΈΣ![]() ΒΡ‘≤ΘΚ________ΘΜ
ΒΡ‘≤ΘΚ________ΘΜ
ΔΎ»γΆΦΘ§…œΖΫ «ΑκΨΕΈΣ![]() ΒΡΑκ‘≤Θ§œ¬ΖΫ «’ΐΖΫ–ΈΒΡ»ΐΧθ±ΏΒΡΓΑ¥ΑΜß–ΈΓΑΘΚ________ΘΜ
ΒΡΑκ‘≤Θ§œ¬ΖΫ «’ΐΖΫ–ΈΒΡ»ΐΧθ±ΏΒΡΓΑ¥ΑΜß–ΈΓΑΘΚ________ΘΜ
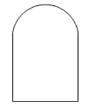
Θ®2Θ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΒψ![]() ΓΔ
ΓΔ![]() Θ§
Θ§![]() «Ήχ±ξΤΫΟφΡΎΒΡΒψΘ§Ν§Ϋ”
«Ήχ±ξΤΫΟφΡΎΒΡΒψΘ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Υυ–Έ≥…ΒΡΆΦ–ΈΈΣ
Υυ–Έ≥…ΒΡΆΦ–ΈΈΣ![]() Θ§Φ«
Θ§Φ«![]() ΒΡΩμΨύΈΣ
ΒΡΩμΨύΈΣ![]() Θ°
Θ°
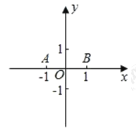
ΔΌ»τ![]() Θ§”Ο÷±≥ΏΚΆ‘≤ΙφΜ≠≥ωΒψ
Θ§”Ο÷±≥ΏΚΆ‘≤ΙφΜ≠≥ωΒψ![]() Υυ‘ΎΒΡ«χ”ρ≤Δ«σΥϋΒΡΟφΜΐΘ®Υυ‘Ύ«χ”ρ”Ο“θ”Α±μ ΨΘ©ΘΜ
Υυ‘ΎΒΡ«χ”ρ≤Δ«σΥϋΒΡΟφΜΐΘ®Υυ‘Ύ«χ”ρ”Ο“θ”Α±μ ΨΘ©ΘΜ
ΔΎ»τΒψ![]() ‘ΎΓ―
‘ΎΓ―![]() …œ‘ΥΕ·Θ§Γ―
…œ‘ΥΕ·Θ§Γ―![]() ΒΡΑκΨΕΈΣ
ΒΡΑκΨΕΈΣ![]() Θ§‘≤–Ρ
Θ§‘≤–Ρ![]() ‘ΎΙΐΒψ
‘ΎΙΐΒψ![]() «“”κ
«“”κ![]() ÷α¥Ι÷±ΒΡ÷±œΏ…œΘ°Ε‘”ΎΓ―
÷α¥Ι÷±ΒΡ÷±œΏ…œΘ°Ε‘”ΎΓ―![]() …œ»Έ“βΒψ
…œ»Έ“βΒψ![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]() Θ§÷±Ϋ”–¥≥ω‘≤–Ρ
Θ§÷±Ϋ”–¥≥ω‘≤–Ρ![]() ΒΡΚαΉχ±ξ
ΒΡΚαΉχ±ξ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ1ΘΜΔΎ![]() ΘΜΘ®2Θ©ΔΌΟφΜΐΈΣ2ΘΜΔΎΒψ
ΘΜΘ®2Θ©ΔΌΟφΜΐΈΣ2ΘΜΔΎΒψ![]() ΒΡΚαΉχ±ξΒΡΖΕΈßΈΣ
ΒΡΚαΉχ±ξΒΡΖΕΈßΈΣ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌΤΫΟφΆΦ–Έ![]() ΒΡΓΑΩμΨύΓ±ΒΡΕ®“εΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΒΡΓΑΩμΨύΓ±ΒΡΕ®“εΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΔΎ»γΆΦΘ§’ΐΖΫ–Έ![]() ΒΡ±Ώ≥ΛΈΣ
ΒΡ±Ώ≥ΛΈΣ![]() Θ§…ηΑκ‘≤ΒΡ‘≤–ΡΈΣ
Θ§…ηΑκ‘≤ΒΡ‘≤–ΡΈΣ![]() Θ§Βψ
Θ§Βψ![]() «Γ―
«Γ―![]() …œ“ΜΒψΘ§Ν§Ϋ”
…œ“ΜΒψΘ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°«σ≥ω
Θ°«σ≥ω![]() ΒΡΉν¥σ÷ΒΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΒΡΉν¥σ÷ΒΦ¥Ω…ΫβΨωΈ ΧβΘ°
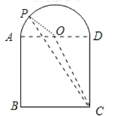
Θ®2Θ©ΔΌ»γΆΦ2©¹1÷–Θ§Βψ![]() Υυ‘ΎΒΡ«χ”ρ «ΆΦ÷–’ΐΖΫ–Έ
Υυ‘ΎΒΡ«χ”ρ «ΆΦ÷–’ΐΖΫ–Έ![]() Θ§ΟφΜΐΈΣ
Θ§ΟφΜΐΈΣ![]() Θ°
Θ°
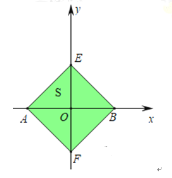
ΔΎ»γΆΦ2©¹2÷–Θ§Β±Βψ![]() ‘Ύ
‘Ύ![]() ÷αΒΡ”“≤ύ ±Θ§Ν§Ϋ”
÷αΒΡ”“≤ύ ±Θ§Ν§Ϋ”![]() Θ§Ής
Θ§Ής![]() ÷α”Ύ
÷α”Ύ![]() Θ°«σ≥ω
Θ°«σ≥ω![]() Μρ
Μρ![]() ±Θ§Βψ
±Θ§Βψ![]() ΒΡΉχ±ξΘ§Φ¥Ω…≈–ΕœΘ§‘ΌΗυΨίΕ‘≥Τ–‘«σ≥ωΒψ
ΒΡΉχ±ξΘ§Φ¥Ω…≈–ΕœΘ§‘ΌΗυΨίΕ‘≥Τ–‘«σ≥ωΒψ![]() ‘Ύ
‘Ύ![]() ÷αΉσ≤ύΒΡ«ι–ΈΦ¥Ω…Θ°
÷αΉσ≤ύΒΡ«ι–ΈΦ¥Ω…Θ°
Θ®1Θ©ΔΌΑκΨΕΈΣ![]() ΒΡ‘≤ΒΡΩμΨύάκΈΣ
ΒΡ‘≤ΒΡΩμΨύάκΈΣ![]() Θ§
Θ§
Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
ΔΎ»γΆΦΘ§’ΐΖΫ–Έ![]() ΒΡ±Ώ≥ΛΈΣ
ΒΡ±Ώ≥ΛΈΣ![]() Θ§…ηΑκ‘≤ΒΡ‘≤–ΡΈΣ
Θ§…ηΑκ‘≤ΒΡ‘≤–ΡΈΣ![]() Θ§Βψ
Θ§Βψ![]() «Γ―
«Γ―![]() …œ“ΜΒψΘ§Ν§Ϋ”
…œ“ΜΒψΘ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°
Θ°
‘Ύ![]() ÷–Θ§
÷–Θ§![]()
![]()
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() ’βΗωΓΑ¥ΑΜß–ΈΓΑΒΡΩμΨύΈΣ
’βΗωΓΑ¥ΑΜß–ΈΓΑΒΡΩμΨύΈΣ![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ![]() Θ°
Θ°
Θ®2Θ©ΔΌ»γΆΦΘ§Βψ![]() Υυ‘ΎΒΡ«χ”ρ «ΆΦ÷–’ΐΖΫ–Έ
Υυ‘ΎΒΡ«χ”ρ «ΆΦ÷–’ΐΖΫ–Έ![]() Θ§ΟφΜΐΈΣ2Θ°
Θ§ΟφΜΐΈΣ2Θ°
ΔΎ»γΆΦΘ§Β±Βψ![]() ‘Ύ
‘Ύ![]() ÷αΒΡ”“≤ύ ±Θ§Ν§Ϋ”
÷αΒΡ”“≤ύ ±Θ§Ν§Ϋ”![]() Θ§Ής
Θ§Ής![]() ÷α”Ύ
÷α”Ύ![]() Θ°
Θ°
![]()
![]() Θ§”÷
Θ§”÷![]()
![]() Θ§
Θ§
![]() Β±
Β±![]() ±Θ°
±Θ°![]() Θ§
Θ§
![]()
![]() Θ§¥Υ ±
Θ§¥Υ ±![]() Θ§
Θ§
Β±![]() ±Θ°
±Θ°![]() Θ§
Θ§
![]()
![]() Θ§¥Υ ±
Θ§¥Υ ±![]() Θ§
Θ§
![]() ¬ζΉψΧθΦΰΒΡΒψ
¬ζΉψΧθΦΰΒΡΒψ![]() ΒΡΚαΉχ±ξΒΡΖΕΈßΈΣ
ΒΡΚαΉχ±ξΒΡΖΕΈßΈΣ![]() Θ°
Θ°


 ≥ε¥Χ100Ζ÷1Κ≈ΨμœΒΝ–¥πΑΗ
≥ε¥Χ100Ζ÷1Κ≈ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
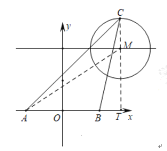
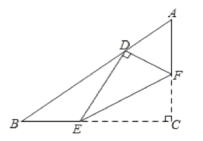
ΓΨΧβΡΩΓΩ»γΆΦ,‘ΎRtΓςABC÷–,ΓœC=90ΓψΘ§AC=3Θ§BC=4Θ§ΒψEΘ§FΖ÷±π‘Ύ±ΏBCΘ§AC…œΘ§―ΊEFΥυ‘ΎΒΡ÷±œΏ’έΒΰΓœCΘ§ ΙΒψCΒΡΕ‘”ΠΒψD«ΓΚΟ¬δ‘Ύ±ΏAB…œΘ§»τΓςEFCΚΆΓςABCœύΥΤΘ§‘ρADΒΡ≥ΛΈΣ___.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2016ΡξΘ§Ρ≥ΤΕάßΜßΒΡΦ“ΆΞΡξ»ΥΨυ¥Ω ’»κΈΣ2500‘ΣΘ§Ά®Ιΐ’ΰΗ°≤ζ“ΒΖω≥÷Θ§ΖΔ’ΙΝΥ―χ÷≥“ΒΚσΘ§ΒΫ2018ΡξΘ§Φ“ΆΞΡξ»ΥΨυ¥Ω ’»κ¥οΒΫΝΥ3600‘ΣΘ°
Θ®1Θ©«σΗΟΤΕάßΜß2016ΡξΒΫ2018ΡξΦ“ΆΞΡξ»ΥΨυ¥Ω ’»κΒΡΡξΤΫΨυ‘ω≥Λ¬ ΘΜ
Θ®2Θ©»τΡξΤΫΨυ‘ω≥Λ¬ ±Θ≥÷≤Μ±δΘ§2019ΡξΗΟΤΕάßΜßΒΡΦ“ΆΞΡξ»ΥΨυ¥Ω ’»κ «ΖώΡή¥οΒΫ4200‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≈ΉΈοœΏy=ax2+bx+c(a<0)Ψ≠ΙΐΒψ(-1,0)Θ§«“¬ζΉψ4a+2b+c>0.“‘œ¬Ϋα¬έ(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2Τδ÷–’ΐ»ΖΒΡΗω ΐ”–( )
A. 1Ηω B. 2Ηω C. 3Ηω D. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
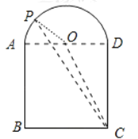
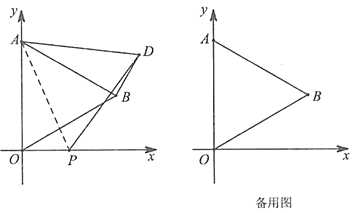
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷Σ![]() «Β»±Ώ»ΐΫ«–ΈΘ§Βψ
«Β»±Ώ»ΐΫ«–ΈΘ§Βψ![]() ΒΡΉχ±ξ «(0Θ§4)Θ§Βψ
ΒΡΉχ±ξ «(0Θ§4)Θ§Βψ![]() ‘ΎΒΎ“ΜœσœόΘ§Βψ
‘ΎΒΎ“ΜœσœόΘ§Βψ![]() «
«![]() ÷α…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”
÷α…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”![]() Θ§≤ΔΑ―
Θ§≤ΔΑ―![]() »ΤΒψ
»ΤΒψ![]() Α¥Ρφ ±’κΖΫœρ–ΐΉΣΘ§ Ι±Ώ
Α¥Ρφ ±’κΖΫœρ–ΐΉΣΘ§ Ι±Ώ![]() ”κ
”κ![]() ÷ΊΚœΘ°Ν§Ϋ”
÷ΊΚœΘ°Ν§Ϋ”![]() Θ§
Θ§![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ°
Θ°
(1)Β±![]() ±Θ§«σ
±Θ§«σ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
(2)‘ΎΒψ![]() ‘ΥΕ·Ιΐ≥Χ÷–Θ§“ά’’ΧθΦΰΥυ–Έ≥…ΒΡ
‘ΥΕ·Ιΐ≥Χ÷–Θ§“ά’’ΧθΦΰΥυ–Έ≥…ΒΡ![]() ΟφΜΐΈΣ
ΟφΜΐΈΣ![]() Θ°
Θ°
ΔΌΒ±![]() ±Θ§«σ
±Θ§«σ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
ΔΎΒ±tΓή0 ±Θ§“Σ Ι![]() Θ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψ
Θ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψ![]() ΒΡΉχ±ξΘ°
ΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
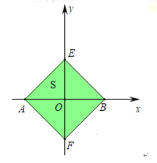
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐΘΚ![]() Θ°
Θ°
Θ®1Θ©«σ÷ΛΘΚΕΰ¥ΈΚ· ΐΒΡΆΦœσ”κx÷α”–ΝΫΗωΫΜΒψΘΜ
Θ®2Θ©Β±Εΰ¥ΈΚ· ΐΒΡΆΦœσ”κx÷αΒΡΝΫΗωΫΜΒψΒΡΚαΉχ±ξΨυΈΣ’ϊ ΐΘ§«“aΈΣΗΚ’ϊ ΐ ±Θ§«σaΒΡ÷ΒΦΑΕΰ¥ΈΚ· ΐΒΡΫβΈω Ϋ≤ΔΜ≠≥ωΕΰ¥ΈΚ· ΐΒΡΆΦœσΘ®≤Μ”ΟΝ–±μΘ§÷Μ“Σ«σ”ΟΤδ”κx÷αΒΡΝΫΗωΫΜΒψAΘ§BΘ®A‘ΎBΒΡΉσ≤ύΘ©Θ§”κy÷αΒΡΫΜΒψCΦΑΤδΕΞΒψD’βΥΡΒψΜ≠≥ωΕΰ¥ΈΚ· ΐΒΡ¥σ÷¬ΆΦœσΘ§Ά§ ±±ξ≥ωAΘ§BΘ§CΘ§DΒΡΈΜ÷ΟΘ©ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Εΰ¥ΈΚ· ΐΒΡΆΦœσ…œ «Ζώ¥φ‘Ύ“ΜΒψP Ι![]() ΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ωΒψPΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ωΒψPΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
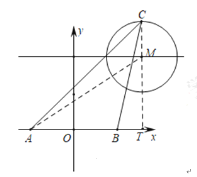
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΒΞΈΜ≥ΛΕ»ΈΣ1ΟΉΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§«ζœΏ «”…ΑκΨΕΈΣ2ΟΉΘ§‘≤–ΡΫ«ΈΣ![]() ΒΡ
ΒΡ![]() Εύ¥ΈΗ¥÷Τ≤Δ ΉΈ≤Ν§Ϋ”Εχ≥…Θ°œ÷”–“ΜΒψP¥”A(AΈΣΉχ±ξ‘≠Βψ)≥ωΖΔΘ§“‘ΟΩΟκ
Εύ¥ΈΗ¥÷Τ≤Δ ΉΈ≤Ν§Ϋ”Εχ≥…Θ°œ÷”–“ΜΒψP¥”A(AΈΣΉχ±ξ‘≠Βψ)≥ωΖΔΘ§“‘ΟΩΟκ![]() ΟΉΒΡΥΌΕ»―Ί«ζœΏœρ”“‘ΥΕ·Θ§‘ρ‘ΎΒΎ2019Οκ ±ΒψPΒΡΉίΉχ±ξΈΣ( )
ΟΉΒΡΥΌΕ»―Ί«ζœΏœρ”“‘ΥΕ·Θ§‘ρ‘ΎΒΎ2019Οκ ±ΒψPΒΡΉίΉχ±ξΈΣ( )
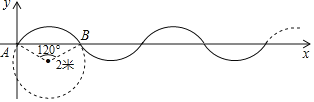
A. ©¹2B. ©¹1C. 0D. 1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
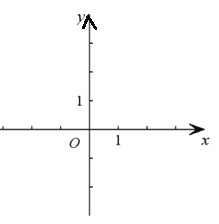
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–(»γΆΦ)Θ§“―÷Σ≈ΉΈοœΏyΘΫx2Θ≠2xΘ§ΤδΕΞΒψΈΣA.
(1)–¥≥ω’βΧθ≈ΉΈοœΏΒΡΩΣΩΎΖΫœρΓΔΕΞΒψAΒΡΉχ±ξΘ§≤ΔΥΒΟςΥϋΒΡ±δΜ·«ιΩωΘΜ
(2)Έ“Ο«Α―“ΜΧθ≈ΉΈοœΏ…œΚαΉχ±ξ”κΉίΉχ±ξœύΒ»ΒΡΒψΫ–Ήω’βΧθ≈ΉΈοœΏΒΡΓΑ≤ΜΕ·ΒψΓ±
ΔΌ ‘«σ≈ΉΈοœΏyΘΫx2Θ≠2xΒΡΓΑ≤ΜΕ·ΒψΓ±ΒΡΉχ±ξΘΜ
ΔΎΤΫ“Τ≈ΉΈοœΏyΘΫx2Θ≠2xΘ§ ΙΥυΒΟ–¬≈ΉΈοœΏΒΡΕΞΒψB «ΗΟ≈ΉΈοœΏΒΡΓΑ≤ΜΕ·ΒψΓ±Θ§ΤδΕ‘≥Τ÷α”κx÷αΫΜ”ΎΒψCΘ§«“ΥΡ±Ώ–ΈOABC «Χί–ΈΘ§«σ–¬≈ΉΈοœΏΒΡ±μ¥ο Ϋ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy=©¹x+4ΒΡΆΦœσ”κΖ¥±»άΐ![]() Θ®kΈΣ≥Θ ΐΘ§«“kΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎAΘ®1Θ§aΘ©Θ§BΘ®bΘ§1Θ©ΝΫΒψΘ§
Θ®kΈΣ≥Θ ΐΘ§«“kΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎAΘ®1Θ§aΘ©Θ§BΘ®bΘ§1Θ©ΝΫΒψΘ§

Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡ±μ¥ο ΫΦΑΒψAΘ§BΒΡΉχ±ξ
Θ®2Θ©‘Ύx÷α…œ’““ΜΒψΘ§ ΙPA+PBΒΡ÷ΒΉν–ΓΘ§«σ¬ζΉψΧθΦΰΒΡΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com