
【题目】(1)材料1:一般地,n个相同因数a相乘:![]() 记为
记为 ![]() 如
如![]() ,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,
,此时,3叫做以2为底的8的对数,记为log28(即log28=3).那么,log39=________,![]() =________;
=________;
(2)材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
①算5!=________;
②已知x为整数,求出满足该等式的![]() .
.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路步数达到10000步及以上可通过微信运动和腾讯基金会向公益活动捐款,如果步数在10000步及以上,每步可捐0.0002元;若步数在10000步以下,则不能参与捐款.
(1)老赵某天的步数为13000步,则他当日可捐多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐了8.4元,且甲的步数=乙的步数=丙步数的3倍,则丙走了多少步?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.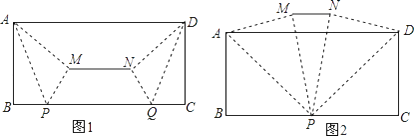
(1)【规律探索】请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)【解决问题】如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,AD⊥BC于点D,以D为圆心DC为半径作⊙D交AD于点G,过点G作⊙D的切线交AB于点F,且F恰好为AB中点. 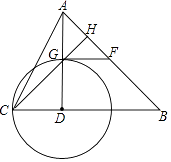
(1)求tan∠ACD的值.
(2)连结CG并延长交AB于点H,若AH=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
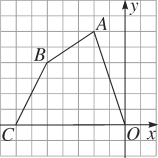
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )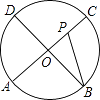
A.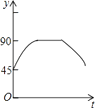
B.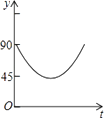
C.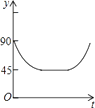
D.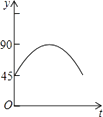
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点都在边长为1的正方形方格纸的格点上,将
的顶点都在边长为1的正方形方格纸的格点上,将![]() 向左平移2格,再向上平移4格.
向左平移2格,再向上平移4格.
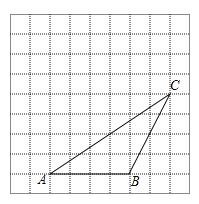
(1)在图中画出平移后的三角形![]() ;
;
(2)在图中画出三角形![]() 的高
的高![]() 、中线
、中线![]() ;
;
(3)图中线段![]() 与
与![]() 的关系是_____;
的关系是_____;
(4)![]() 的面积是_____.
的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.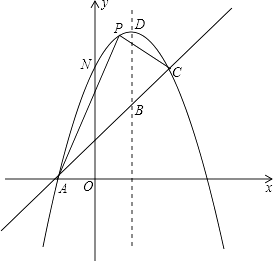
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com