
 小张自主创业销售一种进价为每件20元的新型节能产品,若在国内销售,销售价格y(元/件)与月销售量x(件)的函数关系如图所示.无论销售多少,每月还需支出广告费62500元,设月利润为w1(元)(利润=销售额-成本-广告费).若在国外销售,销售价格为150元/件,受各种因素影响,成本(含进价)为40元/件,当月销量为x(件)时,每月还需缴纳$\frac{1}{100}$x2元的附加费,设月利润为w2(元)(利润=销售额-成本-附加费).
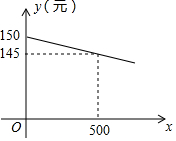
小张自主创业销售一种进价为每件20元的新型节能产品,若在国内销售,销售价格y(元/件)与月销售量x(件)的函数关系如图所示.无论销售多少,每月还需支出广告费62500元,设月利润为w1(元)(利润=销售额-成本-广告费).若在国外销售,销售价格为150元/件,受各种因素影响,成本(含进价)为40元/件,当月销量为x(件)时,每月还需缴纳$\frac{1}{100}$x2元的附加费,设月利润为w2(元)(利润=销售额-成本-附加费).分析 (1)根据待定系数法即可求出y与x的函数关系式,再根据等量关系“利润=销售额-成本-广告费”“利润=销售额-成本-附加费”列出两个函数关系式;
(2)“不赚不赔”即w1=0,列出方程求解可得;
(3)设小张在国内销售a件,则在国外销售数量为(5000-a)件,再根据(1)中两个函数关系式列出在国外销售和国内销售的利润之和的解析式,配方成顶点式,由二次函数的性质可得.
解答 解:(1)设y与x的函数关系式为y=kx+b,由图象得$\left\{\begin{array}{l}{b=150}\\{500k+b=145}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{100}}\\{b=150}\end{array}\right.$,
∴y=-$\frac{1}{100}$x+150,
w1=x(y-20)-62500=-$\frac{1}{100}$x2+130x-62500,
w2=-$\frac{1}{100}$x2+(150-40)x=-$\frac{1}{100}$x2+110x;
(2)令w1=0,则-$\frac{1}{100}$x2+130x-62500=0,
解得x1=12500,x2=500.
故每月的销售量为500件或12500件时,小张不赚不赔;
(3)设小张在国内销售a件,则在国外销售数量为(5000-a)件,
则所获总利润W=-$\frac{1}{100}$a2+130a-62500-$\frac{1}{100}$(5000-a)2+110(5000-a)
=-$\frac{1}{50}$a2+120a+237500
=-$\frac{1}{50}$(a-3000)2+417500,
∵-$\frac{1}{50}$<0,
∴当a=3000时,W最大值=417500,
即在国内销售3000件,在国外销售2000件时,所获总利润最大,为417500元,
答:小张选择在国内销售3000件、在国外销售2000件才能使所获月利润最大.
点评 本题考查了二次函数在实际生活中的应用,考查了一次函数的应用,本题中正确求得函数解析式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 7<b≤8 | B. | 2<b≤3 | C. | 8≤b<9 | D. | 7≤b<8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
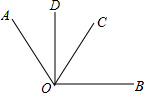 如图,OC是∠AOB的平分线,∠AOD:∠BOD=1:3,若∠COD=25°,则∠AOB的度数为( )
如图,OC是∠AOB的平分线,∠AOD:∠BOD=1:3,若∠COD=25°,则∠AOB的度数为( )| A. | 100° | B. | 80° | C. | 70° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
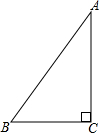 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
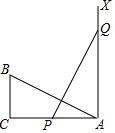 如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=5时,才能使△ABC与△QPA全等.
如图,有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于 AC的射线AX上运动,当AP=5时,才能使△ABC与△QPA全等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com