练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：∠MAN＝60°，点B在射线AM上，AB＝4(如图)．P为直线AN上一动点，以BP为边作等边三角形BPQ(点B，P，Q按顺时针排列)，O是△BPQ的外心．

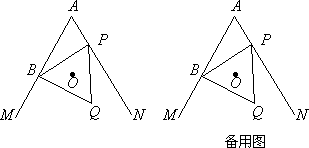
    (1)当点P在射线AN上运动时，求证：点O在∠MAN的平分线上；

    (2)当点P在射线AN上运动(点P与点A不重合)时，AO与BP交于点C，设AP＝x，AC·AO＝y，求y关于x的函数解析式，并写出函数的定义域；

    (3)若点D在射线AN上，AD＝2，圆I为△ABD的内切圆．当△BPQ的边BP或BQ与圆I相切时，请直接写出点A与点O的距离．

    答案：
    解析：

    　　(1)

    　　证明：如图，连结，

    　　是等边三角形的外心，，　　　　1分

    　　圆心角．

    　　当不垂直于时，作，，垂足分别为．

    　　由，且，

    　　，．

    　　．　　　　1分

    　　．　　　　1分

    　　．点在的平分线上．　　　　1分

    　　当时，．

    　　即，点在的平分线上．

    　　综上所述，当点在射线上运动时，点在的平分线上．

    　　(2)

    　　解：如图，

    　　平分，且，

    　　．　　　　1分

    　　由(1)知，，，

    　　，．

    　　，．　　　　1分

    　　．

    　　．．．　　　　1分

    　　定义域为：．　　　　1分

    　　(3)解：①如图，当与圆相切时，；　　　　2分

    　　②如图，当与圆相切时，；　　　　1分

    　　③如图，当与圆相切时，．　　　　2分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：福建省泉州市2012年中考数学试题 题型：044

    已知：A、B、C不在同一直线上．

    (1)若点A、B、C均在半径为R的⊙O上，

    A、B、C如图一，当∠A＝45°时，R＝1，求∠BOC的度数和BC的长度；

    Ⅱ．如图二，当∠A为锐角时，求证sin∠A＝；

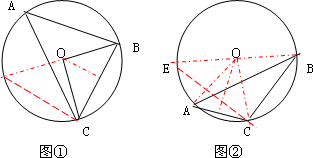
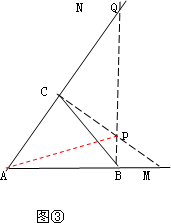
    (2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与点A不重合)滑动，如图三，当∠MAN＝60°，BC＝2时，分别作BP⊥AM，CP⊥AN，交点为点P，试探索：在整个滑动过程中，P、A两点的距离是否保持不变？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2008年山东省临沂市初中毕业升学统一考试、数学试题及答案 题型：044

    已知∠MAN，AC平分∠MAN．

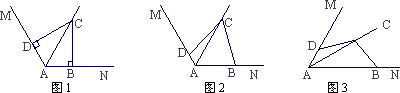
    (1)在图1中，若∠MAN＝120°，∠ABC＝∠ADC＝90°，求证：AB＋AD＝AC；

    (2)在图2中，若∠MAN＝120°，∠ABC＋∠ADC＝180°，则(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

    (3)在图3中：

    ①若∠MAN＝60°，∠ABC＋∠ADC＝180°，则AB＋AD＝________AC；

    ②若∠MAN＝α(0°＜α＜180°)，∠ABC＋∠ADC＝180°，则AB＋AD＝________AC(用含α的三角函数表示)，并给出证明．

    查看答案和解析>>

    同步练习册答案