
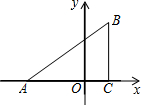
 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.分析 (1)先根据A(-3,1),C(1,0),求出AC进而得出BC=3求出B点坐标,利用待定系数法求出直线AB的解析式即可;
(2)运用相似三角形的性质就可求出点D的坐标;
(3)由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题.
解答 解:(1)∵A(-3,0),C(1,0),
∴AC=4,
∵BC=$\frac{3}{4}$AC,
∴BC=$\frac{3}{4}$×4=3,
∴B(1,3),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{3k+b=0}\\{k+b=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=\frac{9}{4}}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{3}{4}$x+$\frac{9}{4}$;
(2)若△ADB与△ABC相似,
①当点D与C重合时,△ADB∽△ABC,此时D(1,0),
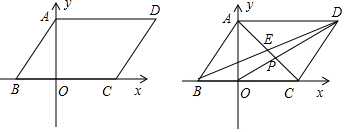
②过点B作BD⊥AB交x轴于D,∴∠ABD=∠ACB=90°,如图1,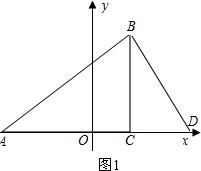
此时 $\frac{AB}{AC}$=$\frac{AD}{AB}$,即AB2=AC•AD.
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴25=4AD,
∴AD=$\frac{25}{4}$,
∴OD=AD-AO=$\frac{25}{4}$-3=$\frac{13}{4}$,
∴点D的坐标为( $\frac{13}{4}$,0).
即:符合条件的D( $\frac{13}{4}$,0)和(1,0)
(3)∵AP=DQ=m,
∴AQ=AD-QD=$\frac{25}{m}$-m.
Ⅰ、若△APQ∽△ABD,如图2,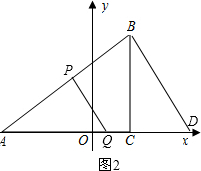
则有 $\frac{AP}{AB}$=$\frac{AQ}{AD}$,
∴AP•AD=AB•AQ,
∴$\frac{25}{4}$m=5( $\frac{25}{4}$-m),
解得m=$\frac{25}{9}$;
Ⅱ、若△APQ∽△ADB,如图3,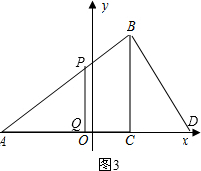
则有 $\frac{AP}{AD}$=$\frac{AQ}{AB}$,
∴AP•AB=AD•AQ,
∴5m=$\frac{25}{4}$( $\frac{25}{4}$-m),
解得:m=$\frac{125}{36}$,
综上所述:符合要求的m的值为 $\frac{125}{36}$或 $\frac{25}{9}$.
点评 本题考查是相似形综合题、待定系数法、相似三角形的判定与性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
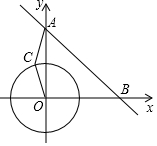 在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.
在平面直角坐标系xOy中,已知点A(0,6),点B(6,0),动点C在以半径为2$\sqrt{2}$的⊙O上,连接OC,AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +10 | -12 | -4 | +8 | -1 | +6 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
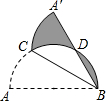 如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.
如图,点C在以AB为直径的半圆弧上,∠ABC=30°,沿直线CB将半圆折叠,点A落在点A′处,A′B和$\widehat{BC}$交于点D,已知AB=6,则图中阴影部分的面积为$\frac{3}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
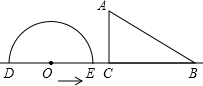 如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.
如图,半圆O直径DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圆O从左到右运动,在运动过程中,点D,E始终在直线BC上,半圆O在△ABC的左侧,当△ABC的一边与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC的三边围成的区域有重叠部分,重叠部分的面积为9π或9$\sqrt{3}$+6π.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com