
要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上,可以证明△EDC≌△ABC,得到ED=AB,因此测得ED的长就是AB的长(如图).判定△EDC≌△ABC的理由是
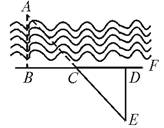
A.边角边公理 B.角边角公理
C.边边边公理 D.斜边直角边公理
科目:初中数学 来源: 题型:
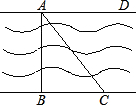 如图,河岸护堤AD、BC互相平行,要测量河两岸相对两树A、B的距离,小赵从B点沿垂直AB的BC方向前进,他手中有足够长的米尺和含有30°角的一块三角板.
如图,河岸护堤AD、BC互相平行,要测量河两岸相对两树A、B的距离,小赵从B点沿垂直AB的BC方向前进,他手中有足够长的米尺和含有30°角的一块三角板.查看答案和解析>>
科目:初中数学 来源: 题型:
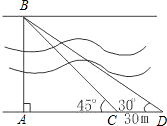 要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.(
要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
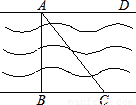
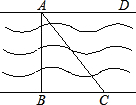 如图,河岸护堤AD、BC互相平行,要测量河两岸相对两树A、B的距离,小赵从B点沿垂直AB的BC方向前进,他手中有足够长的米尺和含有30°角的一块三角板.
如图,河岸护堤AD、BC互相平行,要测量河两岸相对两树A、B的距离,小赵从B点沿垂直AB的BC方向前进,他手中有足够长的米尺和含有30°角的一块三角板.查看答案和解析>>
科目:初中数学 来源:2004-2005学年下学期九年级综合优化测试数学B卷(解析版) 题型:解答题
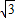 取1.73,精确到0.1 m)
取1.73,精确到0.1 m)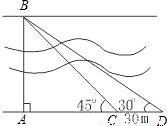
查看答案和解析>>
科目:初中数学 来源:《1.1-1.2 直角三角形的边角关系》2010年同步测试A卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com