
 用长为6m的铝合金制成如图窗框,窗框的上部为由两个正方形组成的矩形,解答下列问题:
用长为6m的铝合金制成如图窗框,窗框的上部为由两个正方形组成的矩形,解答下列问题:分析 (1)根据正方形的性质、结合题意求出AD,根据矩形面积公式计算;
(2)设AB=xcm,根据题意列出二次函数解析式,根据二次函数的性质计算即可.
解答 解:(1)∵铝合金长为6m,AB=1m,
∴AD=(6-3-$\frac{1}{2}$)÷2=$\frac{5}{4}$,
∴此时窗户的透光面积=1×$\frac{5}{4}$=$\frac{5}{4}$(m2);
(2)设AB=xcm,则AD=(6-$\frac{7}{2}$x)÷2,
窗户的透光面积=x×(3-$\frac{7}{4}$x)=-$\frac{7}{4}$x2+3x=-$\frac{7}{4}$(x-$\frac{6}{7}$)2+$\frac{9}{7}$,
则当AB=$\frac{6}{7}$,BC=$\frac{3}{2}$时,窗户的透光面积最大,最大面积是$\frac{9}{7}$平方米.
点评 本题考查的是二次函数的应用,正确列出二次函数解析式、掌握二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正比例函数y1=x的图象与反比例函数y2=$\frac{k}{x}$(k>0)的图象交于A、B两点.
如图,已知正比例函数y1=x的图象与反比例函数y2=$\frac{k}{x}$(k>0)的图象交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
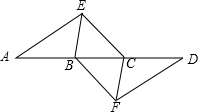 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
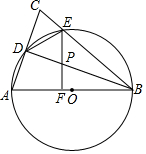 已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.
已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一天 | 3台 | 5台 | 1800元 |
| 第二天 | 4台 | 10台 | 3100元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com