
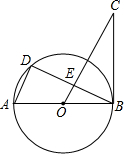
 如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.
如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.分析 (1)由AB为⊙O的直径,可得∠D=90°,继而可得∠ABD+∠A=90°,又由∠DBC=∠A,即可得∠DBC+∠ABD=90°,则可证得BC是⊙O的切线;
(2)根据点O是AB的中点,点E时BD的中点可知OE是△ABD的中位线,故AD∥OE,则∠A=∠BOC,再由(1)∠D=∠OBC=90°,故∠C=∠ABD,由tanC=$\frac{1}{2}$可知tan∠ABD=$\frac{AD}{BD}$=$\frac{1}{2}$,由此可得出结论.
解答 (1)证明:∵AB为⊙O的直径,
∴∠D=90°,
∴∠ABD+∠A=90°,
∵∠DBC=∠A,
∴∠DBC+∠ABD=90°,即AB⊥BC,
∴BC是⊙O的切线;
(2)∵点O是AB的中点,点E时BD的中点,
∴OE是△ABD的中位线,
∴AD∥OE,
∴∠A=∠BOC.、
∵由(1)∠D=∠OBC=90°,
∴∠C=∠ABD,
∵tanC=$\frac{1}{2}$,
∴tan∠ABD=$\frac{AD}{BD}$=$\frac{1}{2}$=$\frac{3}{BD}$,解得BD=6,
∴AB=$\sqrt{{AD}^{2}+{BD}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$.
点评 本题考查的是切线的判定,熟知经过半径的外端且垂直于这条半径的直线是圆的切线是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
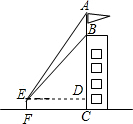 如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com