
����Ŀ����12�֣���ͼ��ʾ�������Ľ����������ߺͳ����ι��ɣ������εij���12 m������4 m������ͼ����ʾ��ֱ������ϵ�������߿�����y=![]() x2+bx+c��ʾ�����������ϵĵ�C��OB��ˮƽ����Ϊ3 m��������OA�ľ���Ϊ
x2+bx+c��ʾ�����������ϵĵ�C��OB��ˮƽ����Ϊ3 m��������OA�ľ���Ϊ![]() m.
m.
��1���������ߵĺ�����ϵʽ�������������D������OA�ľ��룻
��2��һ������������һ�����弯װ����Ϊ6m����Ϊ4m�������������˫������ô���������ܷ�ȫͨ����
��3������������������Ҫ��װ���ŵƣ�ʹ���������ĸ߶���ȣ�����������ĸ߶Ȳ�����8m����ô���ŵƵ�ˮƽ������С�Ƕ����ף�

���𰸡���1�������ߵĺ�����ϵʽΪy=![]() x2+2x+4������D������OA�ľ���Ϊ10 m��(2)���ŵƵ�ˮƽ������С��4
x2+2x+4������D������OA�ľ���Ϊ10 m��(2)���ŵƵ�ˮƽ������С��4![]() m��
m��
��������
������ݵ�B�͵�C�ں���ͼ���ϣ����ô���ϵ�������b��c��ֵ���Ӷ��ó���������ʽ�����ݽ���ʽ����������꣬�ó����ֵ����������ó�������������OA�Ľ���Ϊ��2,0������10,0������Ȼ�������x=2��x=10ʱy��ֵ����6���бȽϴ�С����6��Ϳ���ͨ������6С�Ͳ���ͨ������y=8���뺯�����ó�x��ֵ��Ȼ���������ó���Сֵ��
�����������1������֪��![]() ����������
����������
����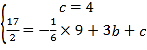 �����
�����![]() ������
������![]()
���ԣ���![]() ʱ��
ʱ��![]()
��![]() ������D������OA�ľ���Ϊ10��
������D������OA�ľ���Ϊ10��
��2������֪������������OA�Ľ���Ϊ��2,0������10,0����
��![]() ʱ��
ʱ��![]() �����Կ���ͨ��
�����Կ���ͨ��
��3����![]() ����
����![]() ���ɵ�
���ɵ�![]() �����
�����![]()
![]() �����ŵƵ�ˮƽ������С��
�����ŵƵ�ˮƽ������С��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺̽������y=|x|��2��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y=|x|��2��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1���ں���y=|x|��2�У��Ա���x����������ʵ����
��2�������y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | 1 | 0 | ��1 | ��2 | ��1 | 0 | m | �� |
��m=�� ����
����A��n��8����B��10��8��Ϊ�ú���ͼ���ϲ�ͬ�����㣬��n=�� ����
��3����ͼ����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣮����������ĵ㣬�����ú�����ͼ����
���ݺ���ͼ��ɵã�
�ٸú�������СֵΪ�� ����
����ֱ֪��![]() �뺯��y=|x|��2��ͼ����C��D���㣬��y1��yʱx��ȡֵ��Χ���� ����
�뺯��y=|x|��2��ͼ����C��D���㣬��y1��yʱx��ȡֵ��Χ���� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ľ�xΪ��������yΪ����.
�Ľ�xΪ��������yΪ����.
��1����a��ȡֵ��Χ��
��2������Oa-3�O+�Oa+2�O��
��3�����̿���������д���������ǰѶ���ʽa2+2ab+b2��a2-2ab+b2������ȫƽ��ʽ�������һ������ʽ������ȫƽ��ʽ�����dz������±��Σ�������һ���ʵ����ʹʽ�г�����ȫƽ��ʽ���ټ�ȥ����ʹ����ʽ�ӵ�ֵ���䣬���ַ��������䷽�����䷽����һ����Ҫ�Ľ���������ѧ�������������Խ�һ�����Ʋ��ֽܷ�Ķ���ʽ�ֽ���ʽ�����ܽ��һЩ��Ǹ����йص�����������ʽ���ֵ����Сֵ�ȣ�
���磺�ֽ���ʽx2+2x-3=(x2+2x+1)-4=(x+1)2-4=(x+1)2-4=(x+1+2)(x+1-2)=(x+3)(x-1)��
�����Ķ��������䷽������������⣺
�ٷֽ���ʽ��m2-4m-5=
�ڵ�a��bΪ��ֵʱ������ʽa2+b2-4a+6b+13=0��
�۵�a��bΪ��ֵʱ������ʽa2-2ab+2b2-2a-4b+10=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC �У�AC=BC����ACB=120������ D ���߶� AB ���˶���D ���� A��B �غϣ������� CD������CDE=30����DE �� BC �ڵ� E������CDE �ǵ��������Σ����ADC �Ķ�����___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ϵ�У���ABC�������������������ΪA����1��2����B����4��1����C����2����2����
��1�������������ϵ��������ABC����y��ԳƵ���A1B1C1��
��2���ֱ�д����A1��B1��C1�����꣮
��3������A1B1C1�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڰ뾶Ϊ5�ġ�O�У�AB��CD�ǻ��ഹֱ�������ң�����ΪP����AB��CD��8����OP�ij�Ϊ( )

A. 3 B. 4 C. 3![]() D. 4
D. 4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ס��ҡ�������������������Ϸ����һ���ɼ�����������ҡ���������ijһ�ˣ��ӵڶ�����ÿһ�ζ��ɳ����߽�������������������˵�ijһ�ˣ���ڶ��δ������ص�������ĸ��ʣ�������������״ͼ�������б����ȷ�ʽ���������̣�
��2�����������n��n��2����������1��ͬ������Ϸ����ô�������δ������ص�������ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������B����O�����ߣ��ڸ�������ȡ��C������AC����O��D������O�İ뾶��6����C=36�������ӻ�AD�ij��ǣ�������

A. ![]() B.
B. ![]() C.
C. ![]() D. 3��
D. 3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com