
分析 (1)设1台彩电的进价为x元,1台冰箱的进价为y元,根据“需要钱数=彩电的单价×彩电台数+冰箱的单价×冰箱台数”即可得出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设购进彩电m台,这批家电的销售利润为W元,根据“总利润=单台彩电的利润×购进彩电的台数+单台冰箱的利润×购进冰箱的台数”即可得出W关于m的一次函数,再根据进货钱数≤19000元可得出关于m的一元一次不等式,解不等式即可得出m的取值范围,结合一次函数的性质即可解决最值问题.
解答 解:(1)设1台彩电的进价为x元,1台冰箱的进价为y元,
依题意得:$\left\{\begin{array}{l}{x+2y=5200}\\{2x+y=5600}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2000}\\{y=1600}\end{array}\right.$.
答:1台彩电的进价为2000元,1台冰箱的进价为1600元.
(2)设购进彩电m台,这批家电的销售利润为W元,则购进冰箱10-m台,
由已知得:W=400m+300(10-m)=100m+3000.
∵2000m+1600(10-m)≤19000,
∴m≤7.5.
∴当m=7时,W取最大值,最大值为3700元.
答:销售完这10台家电后,要使商场获得最大利润,则应购进彩电7台,最大利润为3700元.
点评 本题考查了二元一次方程组的应用、解一元一次不等式以及一次函数的应用,解题的关键:(1)根据数量关系找出关于x、y的二元一次方程组;(2)根据数量关系找出W关于m的一次函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系找出方程(方程组或函数关系式)是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
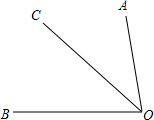 如图所示,OC为∠AOB的角平分线,
如图所示,OC为∠AOB的角平分线,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
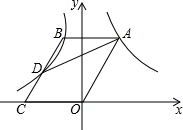 如图,点A在双曲线y=$\frac{6}{x}$(x>0)上,点B在双曲线y=-$\frac{3}{x}$(x<0)上,且AB平行于x轴,BC∥AO交x轴于点C,交双曲线y=-$\frac{3}{x}$(x<0)于点D,连接AD.
如图,点A在双曲线y=$\frac{6}{x}$(x>0)上,点B在双曲线y=-$\frac{3}{x}$(x<0)上,且AB平行于x轴,BC∥AO交x轴于点C,交双曲线y=-$\frac{3}{x}$(x<0)于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 [实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.
[实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com