
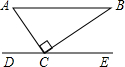
 如图,一直角三角形硬纸板ABC的直角顶点C放在直线DE上,使AB∥DE,若∠BCE=35°,则∠A的度数为
如图,一直角三角形硬纸板ABC的直角顶点C放在直线DE上,使AB∥DE,若∠BCE=35°,则∠A的度数为 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 探索.先在BA上选取点G,使BG=b,连接CG,剪下△BCG并绕点C顺时针旋转90°到△CDH的位置,接下来的问题是:
探索.先在BA上选取点G,使BG=b,连接CG,剪下△BCG并绕点C顺时针旋转90°到△CDH的位置,接下来的问题是:查看答案和解析>>
科目:初中数学 来源: 题型:
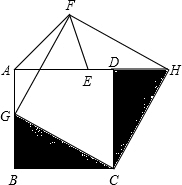
 (2013•泰州一模)一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为
(2013•泰州一模)一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 人教版(新课标2004年初审) 人教实验版 题型:044
如图是用硬纸片做成的两个全等直角三角形和一个等腰直角三角形,尺寸如图所示,请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
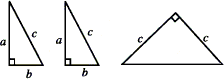
(1)画出示意图,写出它是什么图形;
(2)试用这个图形证明勾股定理;
(3)假设图中的直角三角形有若干多个,你能运用(1)中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼出的示意图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com