
已知如下图,D、E分别是△ABC的AB、AC边的中点,BE、CD相交于点F.
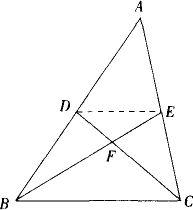
(1)求证:S四边形ADFE=S△BCF;
(2)若SABC=24,求S四边形ADFE.
|
(1)证明:∵D、E分别是AB、AC中点, ∴S△BCD=S△AEB= ∴S△BCD-S△BFD=S△AEB-S△BFD, 即 S四边形ADFE=S△BCF. (2)解:连结DE,易知四边形DBCE是梯形. 设S△BCF=x, ∵S△BED= S△BCD= ∴S△BFD=S△BCD-S△BCF=12-x, ∴SDFE=S△BED-S△BFD=6-(12-x), 根据性质2,有 (SBFD)2=S△BCF·S△DFE, ∴(12-x)2=x[6-(12-x)], 解得x=8. ∴S四边形ADFE=S△BCF=8. 分析:(1)抓住D、E分别为AB、AC中点,用面积关系探求.(2)在(1)的基础上,转求S△BCF通过设未知数,用性质2建立方程进行探求. |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:阅读理解
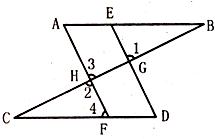 23、阅读下面解答过程,并填空或填理由.
23、阅读下面解答过程,并填空或填理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
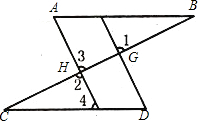
查看答案和解析>>
科目:初中数学 来源:四川省期末题 题型:解答题
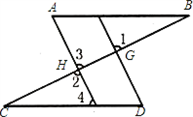
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com