Question

24、在研究三角形内角和等于180°的证明方法时，小胡和小杜分别给出了下列证法．
小胡：在△ABC中，延长BC到D（如左图），
∴∠ACD=∠A+∠B（三角形一个外角等于和它不相邻的两个内角的和）．
又∵∠ACD+∠ACB=180°（平角定义），
∴∠A+∠B+∠ACB=180°（等量代换）．
小杜：在△ABC中，作CD⊥AB（如右图），
∵CD⊥AB（已知），
∴∠ADC=∠BDC=90°（直角定义）．
∴∠A+∠ACD=90°，∠B+∠BCD=90°（直角三角形两锐角互余）．
∴∠A+∠ACD+∠B+∠BCD=180°（等量加等量和相等）．
∴∠A+∠B+∠ACB=180°．
请你对上述两名同学的证法给出评价，并另写出一种你认为较简单的证明三角形内角和定理的方法．

Answer 1

分析：两名同学的证法都不对．因为“三角形一个外角等于和它不相邻的两个内角和”与“直角三角形两锐角互余”都是由三角形内角和定理推导的．

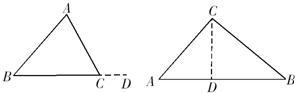
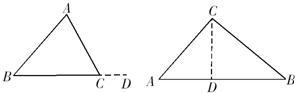
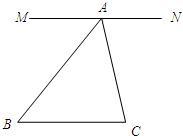解答：解：过点A作直线MN，使MN∥BC
∵MN∥BC
∴∠B=∠MAB，∠C=∠NBC（两直线平行，内错角相等）
∵∠MAB+∠NBC+∠BAC=180°（平角定义）
∴∠B+∠C+∠BAC=180°（等量代换）
即∠A+∠B+∠C=180°．

评价：两位同学都巧妙的通过作辅助线，第一位同学利用平角的定义，第二位同学利用角的和，方法简单，条理清晰．

点评：要证明三角形的内角和等于180°即三角形三个内角的和是平角，就要作辅助线，使得三角形的三个内角的和转化成组成平角的三个角之和．