
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,图象过
,图象过![]() 点,部分图象如图所示,下列判断:①
点,部分图象如图所示,下列判断:①![]() ;②
;②![]() ;③
;③![]() ;④若点
;④若点![]() ,
,![]() 均在抛物线上,则
均在抛物线上,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
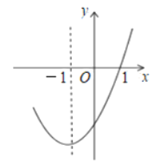
A.1B.2C.3D.4
【答案】B
【解析】
①根据抛物线的开口方向,对称轴的位置和抛物线与y轴交点的位置即可判断![]() 的正负;
的正负;
②根据抛物线与x轴的交点的个数即可判断![]() 与0的大小关系;
与0的大小关系;
③利用a,b,c之间的关系,将b,c换成跟a有关的式子,然后进行判断即可;
④利用二次函数的对称性及二次函数的图象即可作出判断.
①根据抛物线的开口向上可知,![]() ,根据对称轴为
,根据对称轴为![]() ,可知
,可知![]() ,根据抛物线与y轴交点在y轴的负半轴,所以
,根据抛物线与y轴交点在y轴的负半轴,所以![]() ,所以
,所以![]() ,故①错误;
,故①错误;
②根据抛物线与x轴有两个交点,可知![]() ,故②正确;
,故②正确;
③因为二次函数的图象过![]() 点,所以有
点,所以有![]() ,则
,则![]() ,则
,则![]() ,故③正确;
,故③正确;
④利用二次函数的对称性可知![]() 与
与![]() 对应的函数值相等,由二次函数图象可知,
对应的函数值相等,由二次函数图象可知,![]() ,所以
,所以![]() ,故④错误.
,故④错误.
所以正确的②③.
故选:B.


科目:初中数学 来源: 题型:
【题目】△ABC为等腰直角三角形,AB=AC,△ADE为等腰直角三角形,AD=AE,点D在直线BC上,连接CE.
(1)判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;
(2)若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;
(3)若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 不与所在线段端点重合),
不与所在线段端点重合),![]() ,连接
,连接![]() ,射线
,射线![]() ,延长
,延长![]() 交射线
交射线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
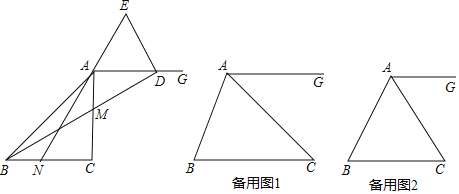
(1)如图,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 的关系:_____;
的关系:_____;![]() 与
与![]() 的位置关系:_____.
的位置关系:_____.
(2)当![]() ,其他条件不变时,
,其他条件不变时,![]() 的度数是多少?(用含
的度数是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
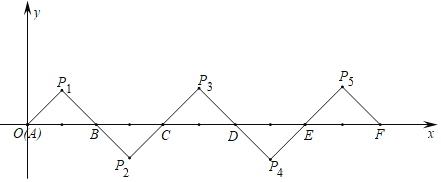
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,把
,把![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() ,得到
,得到![]() ,依此类推,得到的等腰直角三角形的直角顶点
,依此类推,得到的等腰直角三角形的直角顶点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
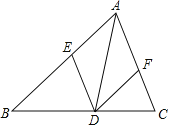
【题目】如图AD是△ABC的角平分线,过点D分别作AC、AB的平行线,交AB于点E,交AC于点F.
(1)求证:四边形AEDF是菱形.
(2)若AF=13,AD=24.求四边形AEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=![]() 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=![]() 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下:如图,两侧最长斜拉索![]() ,
,![]() 相交于点
相交于点![]() ,分别与桥面交于
,分别与桥面交于![]() ,
,![]() 两点,且点
两点,且点![]() ,
,![]() ,
,![]() 在同一竖直平面内.测得
在同一竖直平面内.测得![]() ,
,![]() ,
,![]() 米,请帮助该小组根据测量数据,求斜拉索顶端点
米,请帮助该小组根据测量数据,求斜拉索顶端点![]() 到
到![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com