
【题目】矩形![]() 的对角线交于点
的对角线交于点![]() ,
,![]() .
.
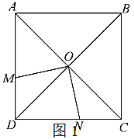
(1)如图1,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,求证:
上,求证:![]() ;
;
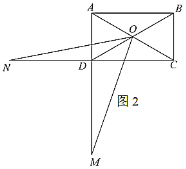
(2)如图2,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 的延长线上,若
的延长线上,若![]() ,求
,求![]() 的值;
的值;
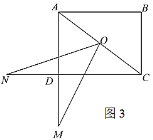
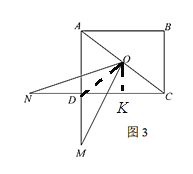
(3)如图3,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 的延长线上,若
的延长线上,若![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用正方形的性质证明![]() 全等即可得到答案,
全等即可得到答案,
(2)在![]() 上取
上取![]() 使得
使得![]() ,证明
,证明![]() ,证明
,证明![]() 为顶角为
为顶角为![]() 的等腰三角形,利用等腰三角形的性质得到
的等腰三角形,利用等腰三角形的性质得到![]() 的数量关系,可得答案,
的数量关系,可得答案,
(3)如图,连接OD,过O作![]() 于
于![]() ,结合已知条件,则得到
,结合已知条件,则得到![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,利用矩形的性质得到:
为半径的圆上,利用矩形的性质得到:![]() 为
为![]() 的中位线,利用勾股定理可得答案.
的中位线,利用勾股定理可得答案.
(1)证明:∵四边形![]() 为矩形,
为矩形,![]()
∴四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,![]()
又![]() ,
,
∴![]()
∴在![]() 和
和![]() 中
中
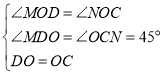
∴![]()
∴![]()
(2)在![]() 上取
上取![]() 使得
使得![]() ,
,
![]() 矩形
矩形![]()
![]()
![]()
∵![]() ,
,
∴![]() ,
,
∴在![]() 与
与![]() 中
中

∴![]() ,
,
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,即
,即![]() 为顶角为
为顶角为![]() 的等腰三角形,
的等腰三角形,
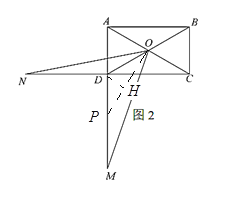
∴设![]() ,过D作
,过D作![]() 于
于![]() ,
,
![]()
∴![]()
![]() .
.
∴![]()
(3)如图,连接OD,过O作![]() 于
于![]() ,
,
![]()
![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,
为半径的圆上,
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]()
![]()
![]() 为矩形对角线的交点,
为矩形对角线的交点, ![]() ,
,
![]() 为
为![]() 的中位线,
的中位线,
![]()
![]()
![]()


科目:初中数学 来源: 题型:
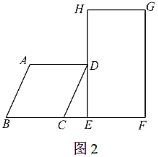
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由49个边长为1的小正方形组成的7×7的正方形网格,小正方形的顶点为格点,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.
均在格点上.

(1)直接写出![]() ________;
________;
(2)点![]() 在网格中的格点上,且
在网格中的格点上,且![]() 是以
是以![]() 为顶角顶点的等腰三角形,则满足条件的点
为顶角顶点的等腰三角形,则满足条件的点![]() 有________个;
有________个;
(3)请在如图所示的网格中,借助矩形![]() 和无刻度的直尺作出
和无刻度的直尺作出![]() 的角平分线,并保留作图痕迹.
的角平分线,并保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形![]() 和平行四边形
和平行四边形![]() (如图1),且
(如图1),且![]() ,
,![]() 在一条直线上,点
在一条直线上,点![]() 落在边
落在边![]() 上.经小明测量,发现此时
上.经小明测量,发现此时![]() 、
、![]() 、
、![]() 三个点在一条直线上,
三个点在一条直线上,![]() ,
,![]() .
.

(1)求![]() 的长度;
的长度;
(2)设![]() 的长度为
的长度为![]() ,
,![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(3)小明接着探究,在保证![]() ,
,![]() 位置不变的前提条件下,从点
位置不变的前提条件下,从点![]() 向右推动正方形,直到四边形
向右推动正方形,直到四边形![]() 刚好变为矩形时停止推动(如图2).若此时
刚好变为矩形时停止推动(如图2).若此时![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
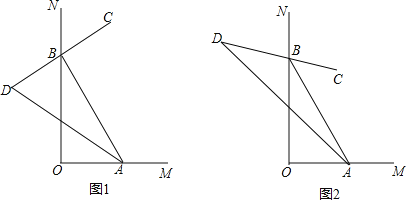
【题目】如图,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(1)如图①,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交于点D.
①若∠BAO=60°,则∠D的大小为 度,
②猜想:∠D的度数是否随A、B的移动发生变化?请说明理由.
(2)如图②,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度,若∠ABC=
∠BAO,则∠D的大小为 度,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度(用含n的代数式表示).
∠BAO,则∠D的大小为 度(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com