
【题目】如图,从热气球C处测得地面A,B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A,D,B在同一直线上,则AB两点的距离是( )
A.200米
B.200 ![]() 米
米
C.220 ![]() 米
米
D.100( ![]() )米
)米
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
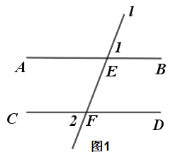
【题目】已知:直线l分别交AB、CD与E、F两点,且AB∥CD.
(1) 说明:∠1=∠2;
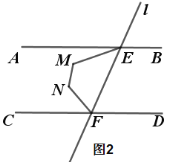
(2) 如图2,点M、N在AB、CD之间,且在直线l左侧,若∠EMN+∠FNM=260°,
①求:∠AEM+∠CFN的度数;
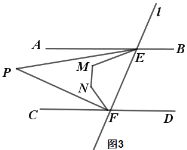
②如图3,若EP平分∠AEM,FP平分∠CFN,求∠P的度数;
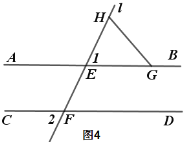
(3) 如图4,∠2=80°,点G在射线EB上,点H在AB上方的直线l上,点Q是平面内一点,连接QG、QH,若∠AGQ=18°,∠FHQ=24°,直接写出∠GQH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题 1、化简
2、若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
(1)先化简,再求值: ![]() ÷(2+
÷(2+ ![]() )
)
(2)若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E,F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5 ![]() ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
(2)如图2,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
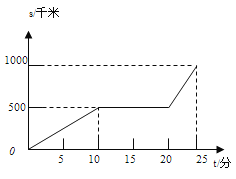
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥ED,CD=BF,若要说明△ABC ≌△EDF,则不能补充的条件是( )

A.AC=EFB.AB=EDC.∠A=∠ED.AC∥EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,进行了如下探索活动.
问题原型:如图(1),在矩形ABCD中,AB=6,AD=8,P、Q分别是AB、AD边的中点,以AP、AQ为邻边作矩形APEQ,连接CE,则CE的长为 (直接填空)
问题变式:(1)如图(2),小明让矩形APEQ绕着点A逆时针旋转至点E恰好落在AD上,连接CE、DQ,请帮助小明求出CE和DQ的长,并求DQ:CE的值.
(2)如图(3),当矩形APEQ绕着点A逆时针旋转至如图(3)位置时,请帮助小明判断DQ:CE的值是否发生变化?若不变,说明理由.若改变,求出新的比值.
问题拓展:若将“问题原型”中的矩形ABCD改变为平行四边形ABCD,且AB=3![]() ,AD=7,∠B=45°,P、Q分别是AB、AD边上的点,且AP=
,AD=7,∠B=45°,P、Q分别是AB、AD边上的点,且AP=![]() AB,AQ=
AB,AQ=![]() AD,以AP、AQ为邻边作平行四边形APEQ.当平行四边形APEQ绕着点A逆时针旋转至如图(4)位置时,连接CE、DQ.请帮助小明求出DQ:CE的值.
AD,以AP、AQ为邻边作平行四边形APEQ.当平行四边形APEQ绕着点A逆时针旋转至如图(4)位置时,连接CE、DQ.请帮助小明求出DQ:CE的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com