
 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过A作AT⊥BE于T点,写出AT+TE与BE之间的数量关系.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过A作AT⊥BE于T点,写出AT+TE与BE之间的数量关系. 分析 结论:BE=2(AT+TE);在线段BT上截取TM=AT,由题意可以证明∠ABM=∠BAM=22.5°,∠MAE=∠MEA=67.5°得到AM=MB=ME即可在证明.
解答 结论:BE=2(AT+TE),理由如下:
证明:在线段BT上截取TM=AT,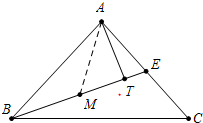
∵AT⊥BE,
∴∠ATM=90°,∠TMA=45°,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵BE平分∠ABC,
∴∠ABM=$\frac{1}{2}$∠ABC=22.5°,
∵∠AMT=∠ABM+∠BAM=45°,
∴∠BAM=22.5°,
∴∠ABM=∠BAM=22.5°,∠MAE=∠MEA=67.5°,
∴MA=MB=ME,
∴BE=2ME=2(MT+TE)=2(AT+TE).
点评 本题考查等腰直角三角形的性质、角平分线的定义,通过辅助线构造等腰直角三角形是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △DBC和△EAC都是等腰直角三角形,斜边BC=$\sqrt{6}$,斜边AC=2,A点在BD上,AE,DC交于F,连接DE,求△DEF的面积.
△DBC和△EAC都是等腰直角三角形,斜边BC=$\sqrt{6}$,斜边AC=2,A点在BD上,AE,DC交于F,连接DE,求△DEF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在讲完《平行线的性质》后,老师出了一道题:如图所示,∠1=65°,∠2=∠65°,∠3=60°,求∠4的度数.小刚看了题目后说:“题中给出∠1和∠2的度数是多余的,因为∠3和∠5是一对同位角,而同位角相等,所以∠5=∠3=60°.又根据对顶角相等得∠4=∠5=60°.你认为小刚的说法对吗?并说明原因.
在讲完《平行线的性质》后,老师出了一道题:如图所示,∠1=65°,∠2=∠65°,∠3=60°,求∠4的度数.小刚看了题目后说:“题中给出∠1和∠2的度数是多余的,因为∠3和∠5是一对同位角,而同位角相等,所以∠5=∠3=60°.又根据对顶角相等得∠4=∠5=60°.你认为小刚的说法对吗?并说明原因.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com