练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，取一张长方形纸片ABCD，按图中所示的方式将纸片折叠，EF、EG为两条褶痕，求∠GEF的度数是
    90°
    90°
    ．
    分析：由根据折叠的性质可得：∠BEF=∠B′EF，∠CEG=∠C′EG，继而可求得∠GEF的度数．
    解答：解：∵根据折叠的性质可得：∠BEF=∠B′EF，∠CEG=∠C′EG，
    ∴∠GEF=∠B′EF+∠C′EG=
    1
    2
    （∠B′EB+∠C′EC）=
    1
    2
    ×180°=90°．
    故答案为：90°．
    点评：此题考查了折叠的性质．此题比较简单，注意掌握折叠前后图形的对应关系．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    综合实践
    问题背景
    某课外兴趣小组在一次折纸活动中，折叠一张带有条格的长方形纸片ABCD（如图1），将点B分别与点A，A1，A2，…，D重合，然后用笔分别描出每条折痕与对应条格所在直线的交点，用平滑的曲线顺次连接各交点，得到一条曲线．
    探索
    如图2，在平面直角坐标系xOy中，将长方形纸片ABCD的顶点B与原点O重合，BC边放在x轴的正半轴上，AB=m，AD=n（m≤n），将纸片折叠，MN是折痕，使点B落在边AD上的E处，过点E作EQ⊥BC，垂足为Q，交直线MN于点P，连接OP
    （1）求证：四边形OMEP是菱形；
    （2）设点P坐标为（x，y），求y与x之间的函数关系式，并写出自变量x的取值范围．（用含m、n的式子表示）
    运用
    （3）将长方形纸片ABCD如图3所示放置，AB=8，AD=12，将纸片折叠，当点B与点D重合时，折痕与DC的延长线交于点F．试问在这条折叠曲线上是否存在K，使得△KCF的面积是△KOC面积的
    53
    ，若存在，写出点K的坐标；若不存在，请说明理由．
    精英家教网

    查看答案和解析>>

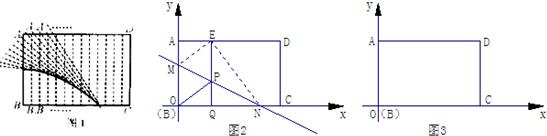
    科目：初中数学 来源：精编教材全解　数学　九年级上册　(配苏科版) 苏科版 题型：044

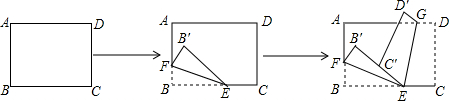
    我们知道了菱形的性质，那想一想如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？下面给出三种方法，

    方法一：将一张长方形的纸横对折，再竖对折，然后沿图中的虚线剪下，打开即是菱形纸片．

    方法二：如图，两张等宽的纸条交叉重叠在一起，重叠的部分ABCD就是菱形．

    方法三：将一张长方形纸对折，再在折痕上取任意长为底边，剪一个等腰三角形，然后打开即是菱形(如图)．试说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源：中学教材全解　七年级数学下　(北京师大版) 北京师大版 题型：059

    让我们一起来进行一个折纸游戏吧！如图所示，取一张长方形的纸片ABCD，将其折叠，使D点与B点重合，EF为折痕，观察图形，图中有全等的三角形吗？如果有，请给出理由；若没有，请说明理由．

    查看答案和解析>>

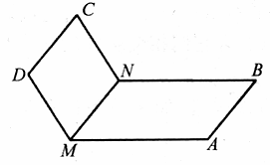
    科目：初中数学 来源： 题型：022

    如图所示，取一张长方形的硬纸ABCD对折，MN是折痕，把面ABNM平摊在桌面上，另一个面CDMN不论怎样改变位置，总有MN∥______，MN∥______，因此______∥______．

    查看答案和解析>>

    科目：初中数学 来源：2010年江苏省镇江市扬中市外国语学校中考数学一模试卷（解析版） 题型：解答题

    综合实践
    问题背景
    某课外兴趣小组在一次折纸活动中，折叠一张带有条格的长方形纸片ABCD（如图1），将点B分别与点A，A1，A2，…，D重合，然后用笔分别描出每条折痕与对应条格所在直线的交点，用平滑的曲线顺次连接各交点，得到一条曲线．
    探索
    如图2，在平面直角坐标系xOy中，将长方形纸片ABCD的顶点B与原点O重合，BC边放在x轴的正半轴上，AB=m，AD=n（m≤n），将纸片折叠，MN是折痕，使点B落在边AD上的E处，过点E作EQ⊥BC，垂足为Q，交直线MN于点P，连接OP
    （1）求证：四边形OMEP是菱形；
    （2）设点P坐标为（x，y），求y与x之间的函数关系式，并写出自变量x的取值范围．（用含m、n的式子表示）
    运用
    （3）将长方形纸片ABCD如图3所示放置，AB=8，AD=12，将纸片折叠，当点B与点D重合时，折痕与DC的延长线交于点F．试问在这条折叠曲线上是否存在K，使得△KCF的面积是△KOC面积的，若存在，写出点K的坐标；若不存在，请说明理由．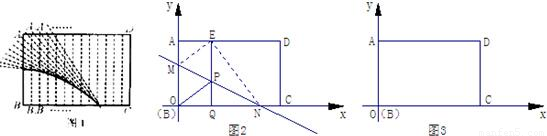

    查看答案和解析>>

    同步练习册答案