
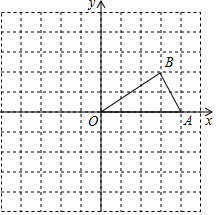
 如图,已知点A,B的坐标分别为(4,0),(3,2).
如图,已知点A,B的坐标分别为(4,0),(3,2).分析 (1)根据网格结构找出点A、O、B向上平移2个单位的对应点A1、O1、B1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、O、B绕点O按逆时针方向旋转90°的对应点A2、O、B2的位置,然后顺次连接即可;
(3)利用勾股定理列式求出OB,再根据AB边扫过的面积等于AB扫过的面积减去OB扫过的面积列式计算即可得解.
解答 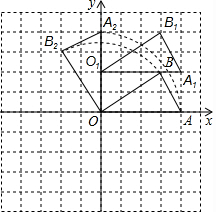 解:(1)△A1O1B1如图所示;
解:(1)△A1O1B1如图所示;
(2)△A2OB2如图所示;
(3)由勾股定理得,OB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
AB边扫过的面积=S扇形AOA2-S扇形BOB2,
=$\frac{90•π•{4}^{2}}{360}$-$\frac{90•π•(\sqrt{13})^{2}}{360}$,
=4π-$\frac{13}{4}$π,
=$\frac{3}{4}$π.
故答案为:$\frac{3}{4}$π.
点评 本题考查了利用平移变换作图,利用旋转变换作图,扇形的面积熟练掌握网格结构,准确找出对应点的位置是解题的关键,难点在于观察出(3)AB扫过的面积等于两个扇形的面积的差.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
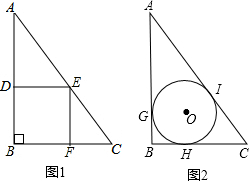 如图,有一块三角形余料ABC,∠B=90°,BC=3m,AB=4m,现有两种余料的再利用方案,分别制作正方形和圆形桌面.
如图,有一块三角形余料ABC,∠B=90°,BC=3m,AB=4m,现有两种余料的再利用方案,分别制作正方形和圆形桌面.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com