
 ;②
;② ;③
;③ ;…用你发现的规律写出:第④个式子是(______),第n个式子是(______);
;…用你发现的规律写出:第④个式子是(______),第n个式子是(______);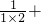
 +
+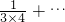 +
+ ;
;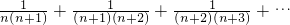 +
+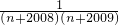 ;
;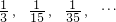 ,猜想第n个数是什么(请用含n的式子表达)把它填入求这组数的前n项和:
,猜想第n个数是什么(请用含n的式子表达)把它填入求这组数的前n项和: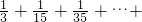 (______)中的括号内,并把这个和式化简.
(______)中的括号内,并把这个和式化简. 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
| 1 |
| (n+2)(n+3) |
| 1 |
| (n+2008)(n+2009) |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com