
【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC= ![]() ,求乙的游泳速度.
,求乙的游泳速度. 
【答案】解:作PH⊥BC于H.
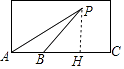
在Rt△PBH中,∵cos∠PBH= ![]() =
= ![]() ,设BH=3k,PB=5k,则PH=4k,
,设BH=3k,PB=5k,则PH=4k,
∵∠PAB+∠PBC=90°,∠PBC+∠BPH=90°,
∴∠BPH=∠PAH,∵∠PHB=∠PHA,
∴△PBH∽△APH,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AH= ![]() k,
k,
∴AB=AH﹣BH= ![]() k﹣3k=
k﹣3k= ![]() ,
,
在Rt△APH中,∵AP=20×1=20,
∴(4k)2+( ![]() k)2=202,
k)2=202,
∴k=3,
∴AB=7,PB=15,
∴乙从A到B的运动时间= ![]() =2s,从B到P的运动时间=22﹣2=20s,
=2s,从B到P的运动时间=22﹣2=20s,
∴乙的游泳速度为 ![]() =0.75米/秒.
=0.75米/秒.
【解析】作PH⊥BC于H.在Rt△PBH中,由cos∠PBH= ![]() =
= ![]() ,设BH=3k,PB=5k,则PH=4k,由△PBH∽△APH,推出
,设BH=3k,PB=5k,则PH=4k,由△PBH∽△APH,推出 ![]() =
= ![]() ,可得AH=
,可得AH= ![]() k,AB=AH﹣BH=
k,AB=AH﹣BH= ![]() k﹣3k=
k﹣3k= ![]() ,在Rt△APH中,AP=20×1=20,利用勾股定理可得(4k)2+(
,在Rt△APH中,AP=20×1=20,利用勾股定理可得(4k)2+( ![]() k)2=202,求出k即可解决问题.
k)2=202,求出k即可解决问题.
【考点精析】利用余角和补角的特征对题目进行判断即可得到答案,需要熟知互余、互补是指两个角的数量关系,与两个角的位置无关.


科目:初中数学 来源: 题型:
【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
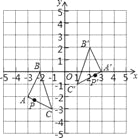
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
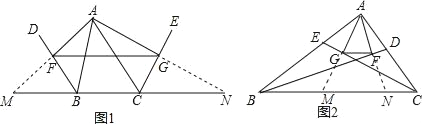
【题目】几何证明:
(1)已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG,延长AF、AG,与直线BC相交.求证:FG=![]() (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图1),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2000名学生每周去图书馆时间的情况,随机调查了其中的100名学生,对这100名学生每周去图书馆的时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周去图书馆的时间在6≤x<8小时的学生人数占20%.根据以上信息及统计图解答下列问题: 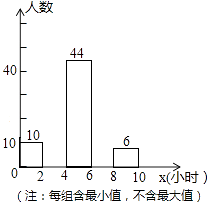
(1)本次调查属于调查,样本容量是;
(2)请补全频数分布直方图中空缺的部分;
(3)若从这100名学生中随机抽取1名学生,求抽取的这个学生每周去图书馆的时间恰好在8﹣10小时的概率;
(4)估计全校学生每周去图书馆的时间不少于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法:①方程x2-3x+2=0是“倍根方程”;②若(x-2)(mx+n)=0是“倍根方程”,则4m2+5mn+n2=0;③若pq=2,则关于x的方程px2+3x+q=0是“倍根方程”;④若方程ax2+bx+c=0是“倍根方程”,且5a+b=0,则方程ax2+bx+c=0的一个根为![]() .其中正确的是____(填序号).
.其中正确的是____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A,B 之间的距离记为|AB|.请回答问题:
(1)直接写出a,b, |AB|的值. a= ,b = , |AB|= ;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(3)若点P在点A的左侧,M、N分别是PA、PB的中点.当点P在点A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com