
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.
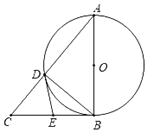
(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
【答案】(1)见解析;(2)tan∠BAC=![]() ;(3)⊙O的半径=2.
;(3)⊙O的半径=2.
【解析】
(1)连接DO,由圆周角定理就可以得出∠ADB=90°,可以得出∠CDB=90°,根据E为BC的中点可以得出DE=BE,就有∠EDB=∠EBD,OD=OB可以得出∠ODB=∠OBD,由等式的性质就可以得出∠ODE=90°就可以得出结论.
(2)由S2=5 S1可得△ADB的面积是△CDE面积的4倍,可求得AD:CD=2:1,可得![]() .则tan∠BAC的值可求;
.则tan∠BAC的值可求;
(3)由(2)的关系即可知![]() ,在Rt△AEB中,由勾股定理即可求AB的长,从而求⊙O的半径.
,在Rt△AEB中,由勾股定理即可求AB的长,从而求⊙O的半径.
解:(1)连接OD,
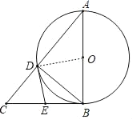
∴OD=OB
∴∠ODB=∠OBD.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°.
∵E为BC的中点,
∴DE=BE,
∴∠EDB=∠EBD,
∴∠ODB+∠EDB=∠OBD+∠EBD,
即∠EDO=∠EBO.
∵BC是以AB为直径的⊙O的切线,
∴AB⊥BC,
∴∠EBO=90°,
∴∠ODE=90°,
∴DE是⊙O的切线;
(2)∵S2=5 S1
∴S△ADB=2S△CDB
∴![]()
∵△BDC∽△ADB
∴![]()
∴DB2=ADDC
∴![]()
∴tan∠BAC==![]() .
.
(3)∵tan∠BAC=![]()
∴![]() ,得BC=
,得BC=![]() AB
AB
∵E为BC的中点
∴BE=![]() AB
AB
∵AE=3![]() ,
,
∴在Rt△AEB中,由勾股定理得
 ,解得AB=4
,解得AB=4
故⊙O的半径R=![]() AB=2.
AB=2.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
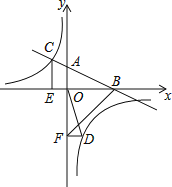
【题目】如图,在平面直角坐标系中,一次函数y=kx+b图象与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 在第二象限内的图象交于点C,CE⊥x轴,tan∠ABO=
在第二象限内的图象交于点C,CE⊥x轴,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数与反比例函数的解析式;
(2)若点D是反比例函数在第四象限内图象上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花卉种植基地准备围建一个面积为100平方米的矩形苗圃园种植玫瑰花,其中一边靠墙,另外三边用29米长的篱笆围成.已知墙长为18米,为方便进入,在墙的对面留出1米宽的门(如图所示),求这个苗圃园垂直于墙的一边长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦节前夕,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销量大,店主决定将玫瑰每枝降价2元促销,降价后80元可购买玫瑰的数量是原来可购买玫瑰数量的1.25倍.
(1)试问:降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于1000元的资金再次购进两种鲜花共180枝,康乃馨进价为6元/枝,玫瑰的进价是5元/枝。试问;至少需要购进多少枝玫瑰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为500元/件,经过两次降价后的价格为405元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为400元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3200元.问第一次降价后至少要售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任大叔决定在承包的荒山上种樱桃树,第一次用1000元购进了一批树苗,第二次又用1000元购进该种树苗,但这次每棵树苗的进价是第一次进价的2倍,购进数量比第次少了100棵;
(1)求第一次每棵树苗的进价是多少元?
(2)一年后,树苗的成活率为85%,每棵樱桃树平均产樱桃30斤,任大叔将两批樱桃树所产樱桃按同一价格全部销售完毕后,获利不低于89800元,求每斤樱桃的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AD为∠CAB的平分线,点O在AB上,⊙O经过点A,D两点,与AC,AB分别交于点E,F
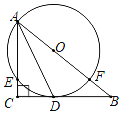
(1)求证:BC与⊙O相切;
(2)若AC=8,AF=10,求AD和BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.
已知:△ABC.
求作:BC边上的高线.
作法:如图,
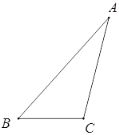
①以点C为圆心,CA为半径画弧;
②以点B为圆心,BA为半径画弧,两弧相交于点D;
③连接AD,交BC的延长线于点E.
所以线段AE就是所求作的BC边上的高线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵CA=CD,
∴点C在线段AD的垂直平分线上( ) (填推理的依据).
∵ = ,
∴点B在线段AD的垂直平分线上.
∴ BC是线段AD的垂直平分线.
∴AD⊥BC.
∴AE就是BC边上的高线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com