
如图,已知正方形
ABCD的边CD在正方形DEFG的边DE上,连接AE、GC.
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论.
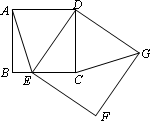
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
|
(1)答:AE^ GC. [证明]延长GC交AE于点H.在正方形ABCD与正方形DEFG中,AD=DC,Ð ADE=Ð CDG=90°,DE=DG,∴△ADE@ △CDG,∴Ð 1=Ð 2,∵Ð 2+Ð 3=90°,
∴Ð 1+Ð 3=90°,∴Ð AHG=180°-(Ð 1+Ð 3)=180°-90°=90°,∴AE^ GC. (2)答:成立. [证明]延长AE和GC相交于点H.在正方形ABCD与正方形DEFG中,AD=DC,DE=DG,Ð ADC=Ð DCB=Ð B=Ð BAD=Ð EDG=90°,
∴Ð 1=Ð 2=90°-Ð 3,∴△ADE@ △CDG, ∴Ð 5=Ð 4,又∵Ð 5+Ð 6=90°, Ð 4+Ð 7=180°-Ð DCE=180°-90°=90°,Ð 6=Ð 7,又 ∵Ð 6+Ð AEB=90° ∴Ð AEB=Ð CEH,∴Ð CEH+Ð 7=90°,∴Ð EHC=90°,∴AE^ GC. |


科目:初中数学 来源: 题型:
 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.2a+
| ||
| 2 |
2a-
| ||
| 2 |
2a+
| ||
| 2 |
2a-
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com