
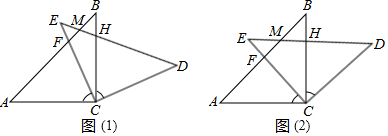
���� ��1������ͬ�ǵ������ȵó���ACE=��DCB�����ݵ���ֱ�������ε����ʵó���A=��D=45�㣬�����ó���ACB�ա�ECD��ASA��������ȫ�������ε����ʣ����ɵó�CF=CH��
��2������AC��MD��CD��AM�����ɵó�ACDM��ƽ���ı��Σ��ٸ���AC=CD�����ɵõ�ACDM�����Σ�
��3�������ı���ACDM�����Σ��õ�CD=AC=$\sqrt{2}$���ٸ��ݡ�D=45�㣬��BCD=45�㣬���ɵó���CDH�ǵ���ֱ�������Σ������õ�AC���ϵĸ�CH=1�����ó��ı���ACDM�����=1��$\sqrt{2}$=$\sqrt{2}$��
���  �⣺��1����ͼ1���ڡ�ACB�͡�ECD�У�
�⣺��1����ͼ1���ڡ�ACB�͡�ECD�У�
�ߡ�ACB=��ECD=90�㣬
���ACE+��ECB=��DCB+��ECB��
���ACE=��DCB��
�֡�AC=CE=CB=CD����ACB=��ECD=90�㣬
���A=��D=45�㣬
�ڡ�ACB�͡�ECD�У�
$\left\{\begin{array}{l}{��A=��D}\\{AC=CD}\\{��ACF=��DCH}\end{array}\right.$��
���ACB�ա�ECD��ASA����
��CF=CH��
��2���ı���ACDM�����Σ�
֤������ͼ2����ACB=��ECD=90�㣬��BCD=45�㣬
���ACE=��ECB=45�㣬
�֡ߡ�E=��B=45�㣬
���ACE=��E����DCB=��B��
��AC��MD��CD��AM��
��ACDM��ƽ���ı��Σ�
�֡�AC=CD��
��ACDM������
��3����ͼ2�����ı���ACDM�����Σ�
��CD=AC=$\sqrt{2}$��
�ߡ�D=45�㣬��BCD=45�㣬
���CHD=90�㣬����CDH�ǵ���ֱ�������Σ�
��AC���ϵĸ�CH=1��
���ı���ACDM�����=1��$\sqrt{2}$=$\sqrt{2}$��
���� ���������������ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ����ε��ж������ʣ�����ֱ�������ε������Լ����ɶ������ۺ�Ӧ�ã��������Ĺؼ������գ�һ���ڱ���ȵ�ƽ���ı��������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC����D�ǵױ�������BC�е��һ���㣬��1=��2��DE=AC�����������������������������ߣ������Եõ�������Щ���ۣ�
��ͼ���ڡ�ABC�У�AB=AC����D�ǵױ�������BC�е��һ���㣬��1=��2��DE=AC�����������������������������ߣ������Եõ�������Щ���ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ε�����������������Ƕ۽� | |
| B�� | ֱ�������ε�����ǻ��� | |
| C�� | ȫ�������εĶ�Ӧ����� | |
| D�� | �����������ߵĴ�ֱƽ����һ��������������һ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�����߸��������12�ߵĵ�A����15�׳�����˿������������߹̶����������̶���֮��ľ��룮
��ͼ��һ�����߸��������12�ߵĵ�A����15�׳�����˿������������߹̶����������̶���֮��ľ��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��4 | B�� | 4��4��9 | C�� | 4��5��9 | D�� | 4��6��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ڢ� | B�� | �ڢۢ� | C�� | �٢� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
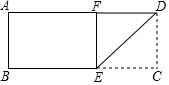 ��ͼһ�ž���ֽƬABCD��AD=10cm������ֽƬ��DE�۵���ʹDC����DA�ϣ���C�Ķ�Ӧ��ΪF����BE=6cm����DE=��������
��ͼһ�ž���ֽƬABCD��AD=10cm������ֽƬ��DE�۵���ʹDC����DA�ϣ���C�Ķ�Ӧ��ΪF����BE=6cm����DE=��������| A�� | $4\sqrt{2}$cm | B�� | 6cm | C�� | 8cm | D�� | 10cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com