
����Ŀ��̽����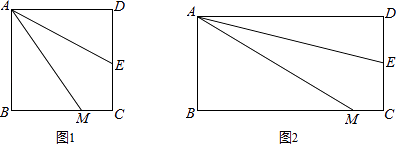
�������龳��
��ͼ1���ı���ABCD�������Σ�M��BC���ϵ�һ�㣬E��CD�ߵ��е㣬AEƽ�֡�DAM��
��1����̽��չʾ��
ֱ��д��AM��AD��MC�����߶ε�������ϵ����
��2������չ���졿
AM=DE+BM�Ƿ�������������������֤����������������˵�����ɣ�
��3�����ı���ABCD�dz��������ȵľ��Σ������������䣬��ͼ2��̽��չʾ��1������2���еĽ����Ƿ��������ֱ������жϣ�����Ҫ֤����
���𰸡�
��1��AM=AD+MC
��2��
AM=DE+BM������
֤��������A��AF��AE����CB���ӳ����ڵ�F����ͼ1��2����ʾ��
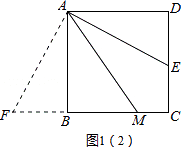
���ı���ABCD�������Σ�
���BAD=��D=��ABC=90�㣬AB=AD��AB��DC��
��AF��AE��
���FAE=90�㣮
���FAB=90�㩁��BAE=��DAE��
�ڡ�ABF�͡�ADE�У�
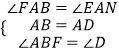
���ABF�ա�ADE��ASA����
��BF=DE����F=��AED��
��AB��DC��
���AED=��BAE��
�ߡ�FAB=��EAD=��EAM��
���AED=��BAE=��BAM+��EAM
=��BAM+��FAB
=��FAM��
���F=��FAM��
��AM=FM��
��AM=FB+BM=DE+BM��
��3��
�ٽ���AM=AD+MC��Ȼ������
֤�����ӳ�AE��BC���ڵ�P����ͼ2��1����
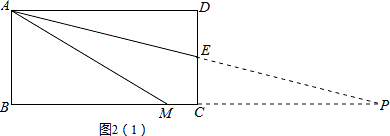
���ı���ABCD�Ǿ��Σ�
��AD��BC��
���DAE=��EPC��
��AEƽ�֡�DAM��
���DAE=��MAE��
���EPC=��MAE��
��MA=MP��
�ڡ�ADE�͡�PCE�У�
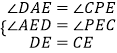
���ADE�ա�PCE��AAS����
��AD=PC��
��MA=MP=PC+MC
=AD+MC��
�ڽ���AM=DE+BM��������
֤��������AM=DE+BM������
����A��AQ��AE����CB���ӳ����ڵ�Q����ͼ2��2����ʾ��
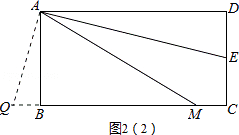
���ı���ABCD�Ǿ��Σ�
���BAD=��D=��ABC=90�㣬AB��DC��
��AQ��AE��
���QAE=90�㣮
���QAB=90�㩁��BAE=��DAE��
���Q=90�㩁��QAB
=90�㩁��DAE
=��AED��
��AB��DC��
���AED=��BAE��
�ߡ�QAB=��EAD=��EAM��
���AED=��BAE=��BAM+��EAM
=��BAM+��QAB
=��QAM��
���Q=��QAM��
��AM=QM��
��AM=QB+BM��
��AM=DE+BM��
��QB=DE��
�ڡ�ABQ�͡�ADE�У�
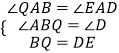
���ABQ�ա�ADE��AAS����
��AB=AD��
��������AB��AD��ì�ܣ��ʼ��費������
��AM=DE+BM������
��������֤�����ӳ�AE��BC���ڵ�N����ͼ1��1����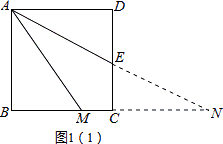
���ı���ABCD�������Σ�
��AD��BC��
���DAE=��ENC��
��AEƽ�֡�DAM��
���DAE=��MAE��
���ENC=��MAE��
��MA=MN��
�ڡ�ADE�͡�NCE�У�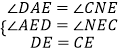
���ADE�ա�NCE��AAS����
��AD=NC��
��MA=MN=NC+MC
=AD+MC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݡ�2014����ú���ᷢչͳ�ƹ�������ʾ��2014���ҹ������Ƽ����Ļ�������ҵ��չ�Ͽ죬����ȫ����ͨ��������7966000�ˣ���7966000�ÿ�ѧ��������ʾΪ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺��1��2x��x+y����3y��x+1������2����a��1��2+��a+1����a��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AD����ô��������һ�������������ж���ABC�ա�ADC���ǣ�������

A. CB=CD B. ��BAC=��DAC C. ��BCA=��DCA D. ��B=��D=90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������2��3��4��4��5��5��5����λ���������ֱ��ǣ�������
A.3.5��5
B.4��4
C.4��5
D.4.5��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BE��CF�ǡ�ABC�ĸ����ཻ�ڵ�P��AQ��BC��CF�ӳ����ڵ�Q������BP=AC��CQ=AB���߶�AP��AQ�Ĺ�ϵ��Σ�˵�����ɡ�
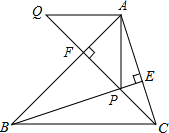
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¶�10�棬�����¶��ǩ�3�棬��ô�����¶ȱ������¶ȸߣ� ��
A.��13��
B.��7��
C.7��
D.13��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.x4+x4=x16
B.����2a��2=��4a2
C.x7��x5=x2
D.m2m=m6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��߶�A'B'�����߶�AB����ƽ�Ƶõ��ģ���֪��A(2��1)�Ķ�Ӧ��ΪA'(3��1)����B�Ķ�Ӧ��ΪB'(4��0)�����B������Ϊ(����)
A.(9��2)B.(1��2)C.(1��3)D.(1��2)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com