
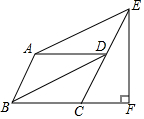
 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
科目:初中数学 来源: 题型:解答题
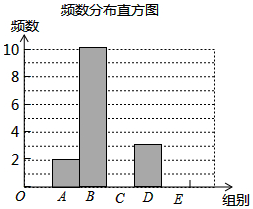 在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
在一次社会调查活动中,小华收集到某“健步走运动”团队中一些成员一天行走的步数,并对这些数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:| 组别 | 步数分组 | 频数 | 频率 |
| A | 5500≤x<6500 | 2 | 0.10 |
| B | 6500≤x<7500 | 10 | 0.50 |
| C | 7500≤x<8500 | a | m |
| D | 8500≤x<9500 | 3 | 0.05 |
| E | 9500≤x<10500 | b | 0.05 |
| 合计 | 5500≤x<10500 | c | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 客户 | 订单(架) | 客户 | 订单(架) |
| 中国国际航空 | 20 | 工银金融租赁有限公司 | 45 |
| 中国东方航空 | 20 | 平安国际融资租赁公司 | 50 |
| 中国南方航空 | 20 | 交银金融租赁有限公司 | 30 |
| 海南航空 | 20 | 中国飞机租赁有限公司 | 20 |
| 四川航空 | 15 | 中银航空租赁私人有限公司 | 20 |
| 河北航空 | 20 | 农银金融租赁有限公司 | 45 |
| 幸福航空 | 20 | 建信金融租赁股份有限公司 | 50 |
| 国银金融租赁有限公司 | 15 | 招银金融租赁公司 | 30 |
| 美国通用租赁公司GECAS | 20 | 兴业金融租赁公司 | 20 |
| 泰国都市航空 | 10 | 德国普仁航空公司 | 7 |
| 订单(架) | 7 | 10 | 15 | 20 | 30 | 50 | |
| 客户(家) | 1 | 1 | 2 | 2 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
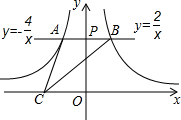 如图,反比例函数y=$\frac{k_1}{x}$和y=$\frac{k_2}{x}$的图象与过y轴正半轴上任意一点M且平行于x轴的直线交于点A和点B,点C是x轴上任意一点,连接AC、BC,若△ABC的面积为8,则k2-k1的值是16.
如图,反比例函数y=$\frac{k_1}{x}$和y=$\frac{k_2}{x}$的图象与过y轴正半轴上任意一点M且平行于x轴的直线交于点A和点B,点C是x轴上任意一点,连接AC、BC,若△ABC的面积为8,则k2-k1的值是16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
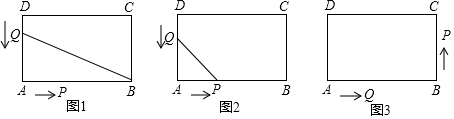
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
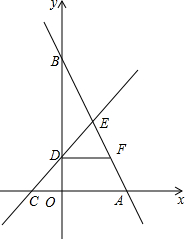 如图,直线y=kx+b分别与x轴、y轴交于点A(2,0)和点B,直线y=x+1分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为CE的中点.
如图,直线y=kx+b分别与x轴、y轴交于点A(2,0)和点B,直线y=x+1分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为CE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com