
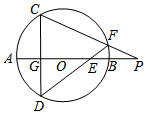
 (如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.
(如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2. 分析 连接FO并延长交⊙O于Q,连接DQ.由FQ是⊙O直径得到∠QFD+∠Q=90°,又由CD⊥AB得到∠P+∠C=90°,然后利用已知条件即可得到∠QFD=∠P,然后即可证明△FOE∽△POF,最后利用相似三角形的性质即可解决问题.
解答 证明:如图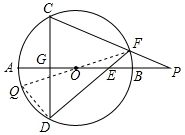 ,连接FO并延长交⊙O于Q,连接DQ.
,连接FO并延长交⊙O于Q,连接DQ.
∵FQ是⊙O直径,
∴∠FDQ=90°.
∴∠QFD+∠Q=90°.
∵CD⊥AB,
∴∠P+∠C=90°.
∵∠Q=∠C,
∴∠QFD=∠P.
∵∠FOE=∠POF,
∴△FOE∽△POF.
∴$\frac{OE}{OF}=\frac{OF}{OP}$.
∴OE•OP=OF2=r2.
点评 此题分别考查了相似三角形的性质与判定、圆周角定理;熟练掌握圆周角定理,证明三角形相似是解决问题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:填空题
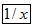 ,能求出输入的不为零的数的倒数(注:有时需先按
,能求出输入的不为零的数的倒数(注:有时需先按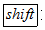 或
或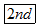 键,才能实现此功能,下面不再说明).例如,输入2,按下键
键,才能实现此功能,下面不再说明).例如,输入2,按下键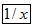 ,则得0.5.现在计算器上输入某数,再依下列顺序按键:
,则得0.5.现在计算器上输入某数,再依下列顺序按键: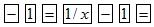 ,在显示屏上的结果是-0.75,则原来输入的某数是5.
,在显示屏上的结果是-0.75,则原来输入的某数是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
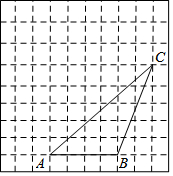 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A2,A4,A6,…分别是射线OM上的点,点A1,A3,A5,…分别是y轴正半轴上的点,△OA1A2,△OA2A3,△OA3A4,…分别是以OA2,OA3,OA4…为底边的等腰三角形,若OM与x轴正半轴的夹角为60°,OA1=1,则可求得点A6的坐标为($\frac{9\sqrt{3}}{2}$,$\frac{27}{2}$),点A2n的坐标为($\frac{1}{2}$$(\sqrt{3})^{2n-1}$,$\frac{1}{2}$$(\sqrt{3})^{2n}$).
如图,点A2,A4,A6,…分别是射线OM上的点,点A1,A3,A5,…分别是y轴正半轴上的点,△OA1A2,△OA2A3,△OA3A4,…分别是以OA2,OA3,OA4…为底边的等腰三角形,若OM与x轴正半轴的夹角为60°,OA1=1,则可求得点A6的坐标为($\frac{9\sqrt{3}}{2}$,$\frac{27}{2}$),点A2n的坐标为($\frac{1}{2}$$(\sqrt{3})^{2n-1}$,$\frac{1}{2}$$(\sqrt{3})^{2n}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com